莫比乌斯反演初步和实际应用

定义和一般形式及其证明

假设有数论函数关系式，则有

此为基本定义，但是看到这个函数也有限制就是必须是数论函数。，也就是定义域为正整数，对应集合为复数的函数。下面是函数的一般形式。

假设d定义在上的复值函数，则有

而这个函数就是莫比乌斯函数，其定义如下：

时，。

，（为互异素数），则

其他情况下

由定义可以得到莫比乌斯函数的两个重要性质：

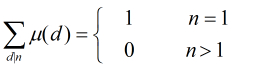
对任意正整数有

证明 :

设有

代入得

由于的限制条件为，所以等式写成:

证明完毕。

代码实现

用线性筛法求莫比乌斯函数，时间复杂度

inline void Init() {
    memset(V, 0, sizeof(V)) ;
    Mu[1] = 1 ; Tot = 0 ;
}

inline void MU() {
    for (int i = 2 ; i < N ; i ++) {
        if (! V[i]) P[++ Tot] = i, Mu[i] = - 1 ;
        for (int j = 0 ; j <= Tot && P[j] < N ; j ++) {
            V[i * P[j]] = 1 ;
            if (i % P[j]) Mu[i * P[j]] = - Mu[i] ;
            else {Mu[i * P[j]] = 0 ; break ; }
        }
    }
}

例题：YY的GCD

给定，求所有的中是质数的点对有多少对。

类似于一个模板题，因为其思维难度不是很大。考虑公式化题目描述，即求：

设为满足的的对数，为满足二点的对数。得到

所以根据莫比乌斯反演定理，得​

而题目要求其是一个质数也就是说

设，则式子变为

于是为了提高速度，可以预处理。于是此题就以较快得速度解决了。

但是如果是多组数据还是有可能会，所以如果想要更快，还可以使用整除分块。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;

typedef long long LL ;
const int MAXN = 10000010 ;

long long T, N, M, V[MAXN], P[MAXN], Mu[MAXN], Tot ;
long long S[MAXN], Ans, G[MAXN] ;

inline long long  Read() {
    long long X = 0, F = 1 ; char ch = getchar() ;
    while (ch > '9' || ch < '0') F = (ch == '-' ? - 1 : 1), ch = getchar() ;
    while (ch >= '0' && ch <= '9') X=(X<<1)+(X<<3)+(ch^48), ch = getchar() ;
    return X * F ;
}

inline void MU() {
    memset(V, 0, sizeof(V)) ;
    Mu[1] = 1 ; Tot = 0 ;
    for (int i = 2 ; i < MAXN ; i ++) {
        if (! V[i]) P[Tot ++] = i, Mu[i] = - 1, G[i] = 1 ;
        for (int j = 0 ; j < Tot && i * P[j] < MAXN ; j ++) {
            V[i * P[j]] = 1 ;
            if (i % P[j]) Mu[i * P[j]] = - Mu[i],
                G[i * P[j]] = Mu[i] - G[i] ; else {
                Mu[i * P[j]] = 0 ; G[i * P[j]] = Mu[i] ;
                break ;
            }
        }
    }
    for (int i = 1 ; i < MAXN ; i ++) S[i] = S[i - 1] + G[i] ;
}

int main() {
    MU() ;
    T = Read() ; while (T --) { 
        Ans = 0 ;
        N = Read(), M = Read() ; 
        for (int i = 1, j ; i <= min(N, M) ; i = j + 1) {
            j = min(N / (N / i), M / (M / i)) ;
            Ans += (N / i) * (M / i) * (S[j] - S[i - 1]) ;
        }
        printf("%lld\n", Ans) ;
    }
}