快速傅里叶变换（后）

单位根

有了幅角和模长，怎么具体的把这个复数写出来呢？三角函数是个很有用的公式，高中知识告诉我们 $sin\theta sin\backslash theta$ 表示当幅角为 $\theta \backslash theta$， 模长为 $11$ 时的 $yy$ 坐标，$cos\theta cos\backslash theta$ 表示 $xx$ 坐标。复平面中 $xx$ 和 $yy$ 分别表示 $aa$ 和 $bb$ 的值，所以我们就可以用三角函数将 $nn$ 次单位根表示出来，${\omega }_n^1=cos\frac{360^{\circ }}{n}+i\times sin\frac{360^{\circ }}{n}\backslash omega\_n^1=cos\backslash frac\{360^\backslash circ\}\{n\}+i\backslash times\; sin\backslash frac\{360^\backslash circ\}\{n\}$，同理 ${\omega }_n^k=cos\frac{360^{\circ }\times k}{n}+i\times sin\frac{360^{\circ }\times k}{n}\backslash omega\_n^k=cos\backslash frac\{360^\backslash circ\backslash times\; k\}\{n\}+i\backslash times\; sin\backslash frac\{360^\backslash circ\backslash times\; k\}\{n\}$，因为之前说过 $kk$ 次方就是将幅角乘 $kk$。我们还需要把公式换成弧度制，因为 C++ 的内置函数是弧度制的。弧度制很简单，只需要记住 $\pi =180^{\circ }\backslash pi=180^\backslash circ$ 即可。于是得到 ${\omega }_n^k=cos\frac{2k\pi }{n}+i\times sin\frac{2k\pi }{n}\backslash omega\_n^k=cos\backslash frac\{2k\backslash pi\}\{n\}+i\backslash times\; sin\backslash frac\{2k\backslash pi\}\{n\}$，这个式子叫做欧拉公式，好像也可以用泰勒展开得到，让人感叹数学的魔幻。

上图中，$OMOM$ 为 $coscos$ 值，$ONON$ 为 $sinsin$ 值。

因为 FFT 中需要正负成对出现的值，所以我们还得看看单位根的正负关系。复数 $a+bia+bi$ 的相反数是 $-a-bi-a-bi$，其几何意义是 $xyxy$ 坐标同时取反，也就是以原点为中心，旋转 $180^{\circ }180^\backslash circ$。用向量表示就是模长相同，方向相反。这很重要，因为我们发现单位圆 $nn$ 等分，当 $nn$ 为偶数时，就能得到 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 对这样互为相反数的点，而它们都可以用单位根表示出来。

如上图，${\omega }_8^1\backslash omega\_8^1$，${\omega }_8^2\backslash omega\_8^2$，${\omega }_8^3\backslash omega\_8^3$ 对应的相反数就是 ${\omega }_8^5\backslash omega\_8^5$，${\omega }_8^6\backslash omega\_8^6$，${\omega }_8^7\backslash omega\_8^7$。

所以我们可以得到当 $nn$ 为偶数时，$-{\omega }_n^k={\omega }_n^{k+\frac{n}{2}}-\backslash omega^k\_n=\backslash omega^\{k+\backslash frac\{n\}\{2\}\}\_\{n\}$ （划重点）。

快速傅里叶变换

直接地说，快速傅里叶变换就是将单位根与其幂带入多项式求点值，并且利用单位根的性质让正负成对的性质一直保持下去，让分治一直成立，从而达到 $O(nlgn)O(nlgn)$ 的时间复杂度。

我们已经知道了当 $nn$ 为偶数时，$-{\omega }_n^k={\omega }_n^{k+\frac{n}{2}}-\backslash omega^k\_n=\backslash omega\_\{n\}^\{k+\backslash frac\{n\}\{2\}\}$，所以带入 $f(-x)=even(x^2)-x\times odd(x^2)f(-x)=even(x^2)-x\; \backslash times\; odd(x^2)$ 得到 $f({\omega }_n^{k+\frac{n}{2}})=even({\omega }_n^{2k})-{\omega }_n^k\times odd({\omega }_n^{2k})f(\backslash omega\_\{n\}^\{k+\backslash frac\{n\}\{2\}\})=even(\backslash omega\_n^\{2k\})-\backslash omega\_n^\{k\}\backslash times\; odd(\backslash omega\_n^\{2k\})$。翻译一下就是求出前 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 个根的 $eveneven$ 和 $oddodd$ 值后，后一半就直接知道了。这个分治是否能一直成立？会不会像实数一样递归一次后就不再是正负成对了？答案是不会，假如我们算的是正的一半（算负的一半也行）：

${\omega }_n^1\backslash omega\_n^\{1\}$，${\omega }_n^2\backslash omega\_n^\{2\}$，$\dots \backslash dots$，${\omega }_n^{\frac{n}{2}}\backslash omega\_n^\{\backslash frac\{n\}\{2\}\}$

它们的幅角分别为：

$\frac{2\pi }{n}\backslash frac\{2\backslash pi\}\{n\}$，$\frac{2\pi }{n}\times 2\backslash frac\{2\backslash pi\}\{n\}\backslash times2$，$\dots \backslash dots$，$\frac{2\pi }{n}\times \frac{n}{2}\backslash frac\{2\backslash pi\}\{n\}\backslash times\; \backslash frac\{n\}\{2\}$（弧度制，$2\pi =360^{\circ }2\backslash pi=360^\backslash circ$）

带入 $eveneven$ 和 $oddodd$ 求点值要先平方，平方相当于幅角翻倍：

$\frac{2\pi }{n}\times 2\backslash frac\{2\backslash pi\}\{n\}\backslash times\; 2$，$\frac{2\pi }{n}\times 4\backslash frac\{2\backslash pi\}\{n\}\backslash times4$，$\dots \backslash dots$，$\frac{2\pi }{n}\times 2\times \frac{n}{2}\backslash frac\{2\backslash pi\}\{n\}\backslash times\; 2\backslash times\backslash frac\{n\}\{2\}$

我们惊奇地发现这 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 个向量平方以后重新将圆等分为了 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 份，当然前提是 $nn$ 为偶数。如何理解？因为 $nn$ 为偶数，所以这前 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 个向量本身平分了 $xx$ 轴上方的半个单位圆。那么平方以后，幅角翻倍，就变成平分整个单位圆了。所以如果 $\frac{n}{2}\backslash frac\{n\}\{2\}$ 还是偶数，就能继续分治下去，因为既然是平分单位圆，那就还是正负成对的。

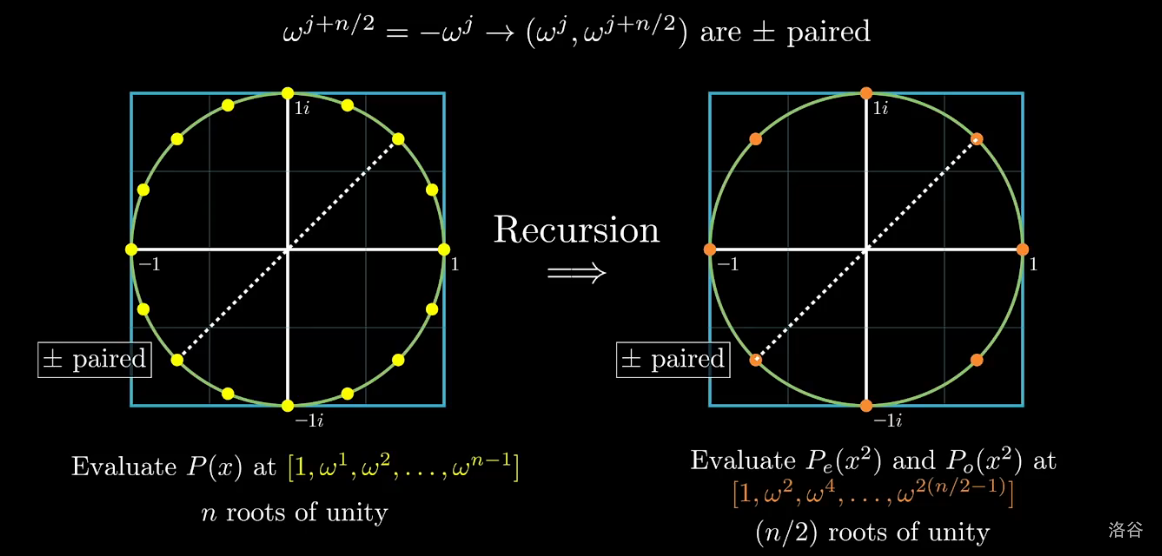
因此，我们可以将多项式变成 $22$ 的幂个项，多的项就当系数为 $00$，因为这样就能分治到底了，实现起来非常方便并且时间复杂度也是不变的。

例如多项式 $x^3+3x^2+2x+4x^3+3x^2+2x+4$ 应补成 $0x^4+x^3+3x^2+2x+40x^4+x^3+3x^2+2x+4$，因为 $4=2^{2}4=2^2$。

快速傅里叶逆变换

我们已经讲完了如何使用单位根使分治成立，从而在 $O(nlgn)O(nlgn)$ 内将系数表示法转换成点值表示法。但反过来怎么办呢？如何在 $O(nlgn)O(nlgn)$ 内将点值表示法转换成系数表示法？

点值的计算可以写成矩阵乘法的形式，矩阵乘法很简单，不会可以点这里。

其中最左边的矩阵是带入的单位根，每个项括号外有裹了个次方是因为多项式每项变量的次数是不一样的。$a_{0}a\_0$ 到 $a_{n-1}a\_\{n-1\}$ 是多项式的系数。$y_{0}y\_0$ 到 $y_{n-1}y\_\{n-1\}$ 是算出来的点值。

假如我们已经通过点值表示法的多项式乘法得到了结果多项式的点值，也就是说 $y_{0}y\_0$ 到 $y_{n-1}y\_\{n-1\}$ 是已知的。需要求结果多项式的系数，也就是说 $a_{0}a\_0$ 到 $a_{n-1}a\_\{n-1\}$ 是未知的。这里要用一些线性代数的知识。设 $AA$，$BB$ 和 $CC$ 都是矩阵，且 $A\ast B=CA\; *\; B=C$（矩阵乘法记做 $\ast *$），那么就有 $A^{-1}\ast C=BA^\{-1\}*C=B$，其中矩阵 $A^{-1}A^\{-1\}$ 为矩阵 $AA$ 的逆矩阵。注意这里的 $-1-1$ 不是次方的意思，只是一种标记方法，表示逆矩阵。

所以我们只需要求出最左边的矩阵的逆矩阵就能通过乘以点值矩阵得到系数矩阵了。而这个工作数学家们已经帮我们完成了，涉及亿点线性代数，我就不展开了，想看完整证明的同学可以点这里。

求其逆矩阵最后的结果是：

上加一线表示共轭，也就是复数含 $ii$ 的项取反，前面的 $\frac{1}{n}\backslash frac\{1\}\{n\}$ 表示矩阵内的每个项都除以 $nn$。总体来说，其逆矩阵就是每项取共轭，再除以 $nn$。

点值矩阵乘以这个逆矩阵得到的矩阵每项再除以 $nn$ 就是系数矩阵，但这个工作也是 $O(n^2)O(n^2)$ 的，如何加速？细心的读者可能已经发现了，这个过程和傅里叶快速变换是一样的，完全可以用相同的分治来加速，因为共轭实质上就是按 $xx$ 轴翻折，单位圆上单位根的性质不变。代码实现中两者只有一行语句的差别，也就是单位根含 $ii$ 项的正负号。

代码实现

洛谷 P3803 FFT

#include <bits/stdc++.h>
#define N 5000000
#define err 1e-6
using namespace std;

int n, m;
const double pi = acos(-1.0);
complex<double> a[N], b[N]; 

void fft(complex<double> *a,int len,int inv){
	if(len==1)return;
	complex<double> e[len/2],o[len/2];
	for(int i=0;i<len;i+=2)
		e[i/2]=a[i],o[i/2]=a[i+1];
	fft(e,len/2,inv); fft(o,len/2,inv);
	complex<double> wn(cos(2*pi/len),sin(2*pi/len)*inv),wk(1,0);
	for(int i=0;i<len/2;i++,wk*=wn)
		a[i]=e[i]+wk*o[i],
		a[i+len/2]=e[i]-wk*o[i];
}

int main(){
	cin>>n>>m;
	for(int i=0,buf;i<=n;i++)cin>>buf,a[i].real(buf);
	for(int i=0,buf;i<=m;i++)cin>>buf,b[i].real(buf);
	int len=1; while(len<n+m+1)len<<=1;
	fft(a,len,1); fft(b,len,1);
	for(int i=0;i<len;i++)a[i]*=b[i];
	fft(a,len,-1);
	for (int i=0;i<=n+m;++i)
		printf("%.0f ",a[i].real()/len);
	return 0;
}

参考资料

Fast Fourier Transform (2020), Youtube [online]. Available from: https://www.youtube.com/watch?v=h7apO7q16V0&feature=emb_logo [Accessed on June 1 2022]

一小时学会快速傅里叶变换 (2022), zhihu [online]. Available from: https://zhuanlan.zhihu.com/p/31584464 [Accessed on May 31 2022]

快速傅里叶变换 (2022), zhihu [online]. Available from: https://zhuanlan.zhihu.com/p/347091298 [Accessed on May 31 2022]

图片均来源于网络，侵权必删！