题解 | #小白月赛 44 题解#

小白月赛 44 民间题解（A $\sim \backslash sim$ F）

Problem A

由正确题意，考虑如何找到所有的极长段：

如下图

  3  3  3
 2  2  2
1  1  1

可以观察到找到每两个上升段之间的下坡，这是区分不同“上升段”之间的标志，这也是一个常用的办法。

最后一段可以特殊处理，比如令 $a_{n+1}=-\mathrm{\infty }a\_\{n+1\}=-\backslash infin$ 是一种不错的选择。

至此我们已经成功分离出每一个上升段：

假设某一个上升段左端点是 $LL$，右端点是 $RR$。那么由题意，如果设目前最大上升幅度为 $LenLen$。

初始化：$Len=-1Len=-1$

分三种情况讨论：

1. $Len=-1Len=-1$ 或 $a_R-a_L>Lena\_R-a\_L>Len$：严格更优解。直接清空当前答案的存储序列，加入新解。

2. $a_R-a_L=Lena\_R-a\_L=Len$：一样优的解：将这组 $(L,R)(L,R)$ 数对加入答案。

3. ：无效解，舍去。

官方题解中的实现运用了 vector 和 pair 等奇技淫巧，可能对小白不太友好。

那么这里我也写了一个较为正常的实现办法。主要实现办法是用 $b[0]b[0]$ 表示长度，$b[\text{奇数}]b[\backslash text\{奇数\}]$ 表示左端点，$b[\text{偶数}]b[\backslash text\{偶数\}]$ 表示右端点。

a[N + 1] = -1; int pre = 1;
for (int i = 2; i <= N + 1; ++i)
  if (a[i - 1] > a[i]) { // pre ~ i - 1
    if (!b[0] || a[i - 1] - a[pre] > a[b[2]] - a[b[1]])
      b[0] = 2, b[1] = pre, b[2] = i - 1;
    else if (a[i - 1] - a[pre] == a[b[2]] - a[b[1]])
      b[++b[0]] = pre, b[++b[0]] = i - 1;
    pre = i;
  }
for (int i = 1; i <= b[0]; ++i)
  print(b[i]);

Problem B

写一种两遍 for 循环模拟的思路：（第一遍标记被保护的格子，第二遍统计未被标记的植物格子）

bool ok[N][N];
for (int i = 1; i <= n; ++i)
  for (int j = 1; j <= n; ++j)
    for (int k = 0; k < 8; ++k) {
      int ni = i + dx[k], nj = j + dy[k];
      ok[ni][nj] = (ju[i][j] == '*');
    }
int ans = 0;
for (int i = 1; i <= n; ++i)
  for (int j = 1; j <= n; ++j)
    ans += (ju[i][j] == 'P' && !ok[i][j]);

Problem C

简单解析一下这个五折出点的问题。（下文中 “$\sim \backslash sim$” 表示 “相当于” 的意思）

充值 $1R\sim 1001R\backslash sim100$ 红点这点大家都可以接受吧。

每 $1010$ 红点 $\sim 1\backslash sim1$ 经验，由题意可得。

那么这个问题可以转化成 $1R\sim 1001R\backslash sim100$ 红点 $\sim 10\backslash sim10$ 经验。

再算上充值返点，$1R\sim \min \{10000,100\times (M-1)\}1R\backslash sim\backslash min\backslash \{10000,100\backslash times(M-1)\backslash \}$ 绿 $\sim \min (1000,10\times (M-1))\backslash sim\backslash min(1000,10\backslash times(M-1))$ 经验。

那么知道这个之后，不难得到直接用 RMB 转换成经验。

另外还有就是红点可以用于出售，这里按照五折出点来计算，每次 $2R\sim 2002R\backslash sim200$ 红 $\sim 1R\backslash sim1R$。

所以 RMB 数每次会除以 $22$ 并向下取整。

综上不难得到代码。考虑到本题考察的是数学能力而非模（bian）拟（cheng）能力。据此直接模拟题意不被提倡，另外如果写法正确也完全不会被所谓“卡精度”。下面给出两篇分别使用 int 和 double 的示例代码。

#include<cstdio>
#include<cassert>
#define int long long
int init(){
	char c = getchar();
	int x = 0, f = 1;
	for (; c < '0' || c > '9'; c = getchar())
		if (c == '-') f = -1;
	for (; (c >= '0' && c <= '9') || c == '.'; c = getchar())
		if (c != '.') x = (x << 1) + (x << 3) + (c ^ 48);
	return x * f;
}
void print(int x){
	if (x < 0) x = -x, putchar('-');
	if (x > 9) print(x / 10);
	putchar(x % 10 + '0');
}
int mn(int x, int y){
	return x < y ? x : y;
}
signed main(){
	int T = init();
	while (T--) {
		int n = init(), m = init();
		int ans = 0;
		while (n) {
			ans += n * 10 + mn(1000, n * (m - 10));
			n >>= 1;
		}
		print(ans), putchar('\n');
	}
}

用 double：

double op(int n, double m){
  double ans = 0;
  while (n > 0) {
    ans += n * 10 + min(1000.0, (n*10*(m-1)));
    n /= 2;
  }
  return ans;
}

Problem D

以 $123\times 45123\backslash times45$ 为例：

正常的写法如上图所示，所以是依次计算：

$123\times 45=(123\times 40)+(123\times 5)=(100+20+3)\times 40+(100+20+3)\times 5123\backslash times45=(123\backslash times40)+(123\backslash times5)=(100+20+3)\backslash times40+(100+20+3)\backslash times5$

然后之前说的相乘改成相加就是将这里的乘号全部改成加号即可。事实上样例解释是题目做法的提示：

$\Rightarrow 140+105+60+25+43+8=123\times 2+45\times 3=246+135=381\backslash Rightarrow140+105+60+25+43+8=123\backslash times2+45\backslash times3=246+135=381$。

Problem E

由于每个黑点相邻全是白点。

据此直径（最长链）长度只能是 $11$。

最后 dfs 找一下所有黑点个数即可。

由于每条起点、终点都是黑点的链是直径（相当于充要条件）。

所以答案就是 ${\displaystyle \frac{Cnt(Cnt+1)}{2}}\backslash dfrac\{Cnt(Cnt+1)\}\{2\}$。

Problem F

Back $\Leftarrow \backslash Leftarrow$

问题模型

你获得了 $nn$ 条链，第 $ii$ 条链的长度是 $a_{i}a\_i$。

给这 $\sum a_i\backslash sum\; a\_i$ 个点再连上 $n-1n-1$ 条边，使得它们构成一个包含 $\sum a_i\backslash sum\; a\_i$ 个结点的“大树”。

请输出最终 可能 成为“大树”重心的结点的个数。

模型分析

对于第 $ii$ 条链的第 $jj$ 个结点（以下简称点 $(i,j)(i,j)$）：

• 首先很明显根据“重心”定义，最优策略是把剩下 $n-1n-1$ 条链全部作为子树挂上去。

• 进而分析有解的条件，也就是说：

• 记 $x=j-1,y=a_i-jx=j-1,y=a\_i-j$（第 $jj$ 个点之前、第 $jj$ 个点之后的结点数）

• 所以 $a_1,a_2,\cdots ,a_{i-1},a_{i+1},\cdots ,a_n,x,ya\_1,a\_2,\backslash cdots,a\_\{i-1\},a\_\{i+1\},\backslash cdots,a\_n,x,y$ 共同构成点 $(i,j)(i,j)$ 的子树。

据此只需要判断：

$\max \{a_1,a_2,\cdots ,a_{i-1},a_{i+1},\cdots ,a_n,x,y\}\le \lfloor {\displaystyle \frac{\sum a_i}{2}}\rfloor \backslash max\backslash \{a\_1,a\_2,\backslash cdots,a\_\{i-1\},a\_\{i+1\},\backslash cdots,a\_n,x,y\backslash \}\backslash le\backslash left\backslash lfloor\backslash dfrac\{\backslash sum\; a\_i\}\{2\}\backslash right\backslash rfloor$

不妨考虑拆解这个式子：

$\{\begin{array}{c}\max \{a_1,a_2,\cdots ,a_{i-1},a_{i+1},\cdots ,a_n\}\le \lfloor {\displaystyle \frac{\sum a_i}{2}}\rfloor \\ \max \{x,y\}\le \lfloor {\displaystyle \frac{\sum a_i}{2}}\rfloor \end{array}\backslash begin\{cases\}\backslash max\backslash \{a\_1,a\_2,\backslash cdots,a\_\{i-1\},a\_\{i+1\},\backslash cdots,a\_n\backslash \}\backslash le\backslash left\backslash lfloor\backslash dfrac\{\backslash sum\; a\_i\}\{2\}\backslash right\backslash rfloor\backslash \backslash \backslash max\backslash \{x,y\backslash \}\backslash le\backslash left\backslash lfloor\backslash dfrac\{\backslash sum\; a\_i\}\{2\}\backslash right\backslash rfloor\backslash end\{cases\}$

第一个式子可以考虑预处理除去 $a_{i}a\_i$ 之后的序列 $\max \backslash max$ 值，$O(n)O(n)$ 扫描即可。

第二个式子可以考虑对于一个 $a_{i}a\_i$ 批量计算（在满足了一式的前提下），考虑奇偶分讨：

由图示结论可得，$a_{i}a\_i$ 的贡献是：

• $a_{i}a\_i$ 为偶数：$\min (\lfloor {\displaystyle \frac{\sum _{j\mathrm{\ne }i}{a}_j}{2}}\rfloor \times 2+2,a_i)\backslash min\backslash left(\backslash left\backslash lfloor\backslash dfrac\{\backslash sum\backslash limits\_\{j\backslash ne\; i\}a\_j\}\{2\}\backslash right\backslash rfloor\backslash times2+2,a\_i\backslash right)$

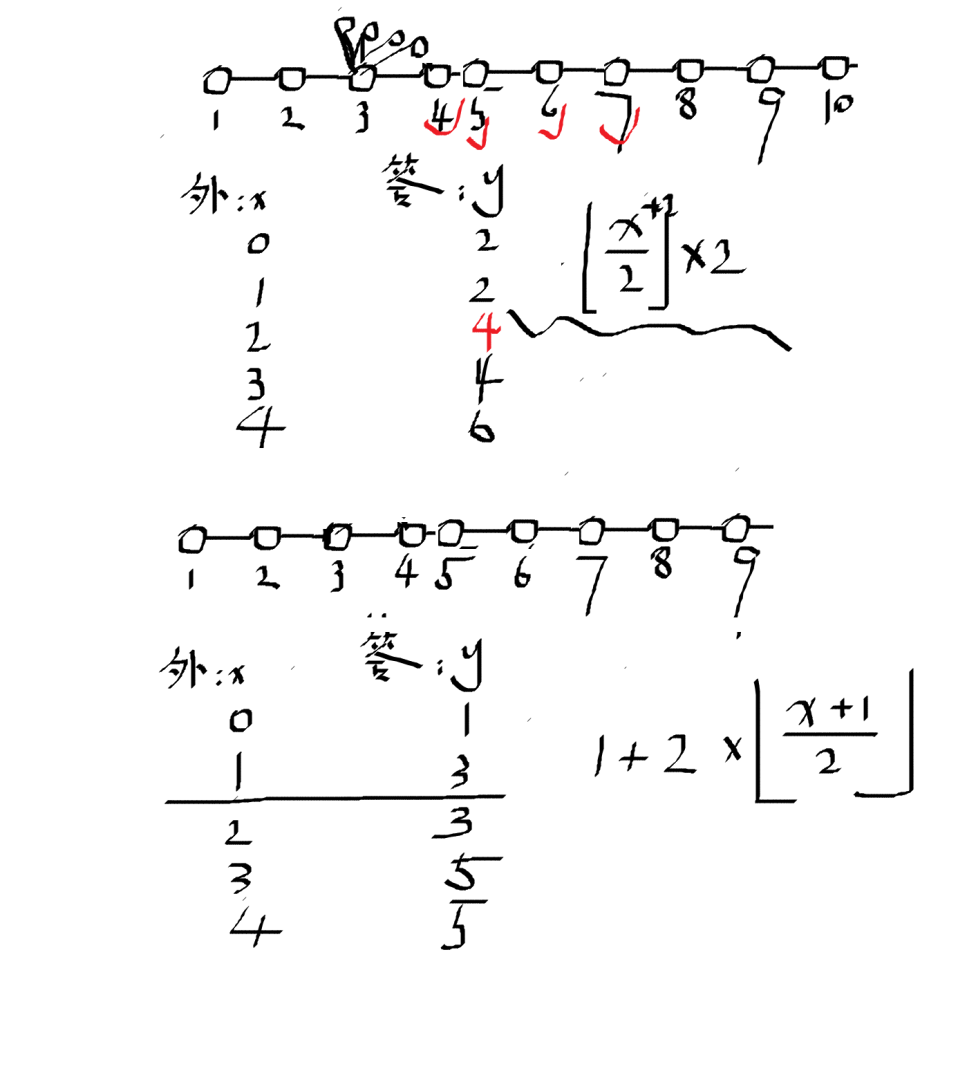
• $a_{i}a\_i$ 为奇数：$\min (\lceil {\displaystyle \frac{\sum _{j\mathrm{\ne }i}{a}_j}{2}}\rceil \times 2+1,a_i)\backslash min\backslash left(\backslash left\backslash lceil\backslash dfrac\{\backslash sum\backslash limits\_\{j\backslash ne\; i\}a\_j\}\{2\}\backslash right\backslash rceil\backslash times2+1,a\_i\backslash right)$