数论笔记本
转自Armin’s blog
数论是个好东西。
欧几里德算法(gcd)
- 欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。
定理
- gcd(a,b)=gcd(b,a mod b)
- 特别的: gcd(a,0)=a
证明
充分性
设c为a,b的公约数
∵a∣c,KaTeX parse error: Expected 'EOF', got '&' at position 4: b|c&̲emsp; &ems… (|:整除)
又 ∵a=kb+(a mod b),即 a mod b=a−kb
∴(a mod b)∣c
必要性
设 c为 b, a mod b的公约数
KaTeX parse error: Expected 'EOF', got '&' at position 14: \because b|c,&̲emsp;(a mod b)∣c
又 ∵a=kb+(a mod b)
∴a∣c
代码
int gcd(int a, int b){
return b? gcd(b, a % b):a;
}
扩展欧几里德算法
- 扩展欧几里德算法是用来在已知a, b求解一组x,y,使它们满足等式:$ ax+by = gcd(a, b)$(解一定存在,根据数论中的相关定理)。扩展欧几里德常用在求解模线性方程及方程组中。
代码
因为不好描述,所以先给出代码。
int x,y;
int exgcd(int a,int b){ //拓展欧几里德算法,求出的x,即为a%b下a的逆元
if(b==0){
x=1;y=0;
return a;
}
int r=exgcd(b,a%b);
int c=x; //c只是为了储存x的值
x=y;
y=c-a/b*y;
return r;
}
证明
递归之后,$ a’=b , b’=a % b = a-a/b \times b $ (这里的/为计算机里的除法)
a′x+b′y=gcd(a,b)
代入化简$\Rightarrow ay+b(x-a/b \times y) = gcd(a,b) $
又 ∵ax+by=gcd(a,b)
KaTeX parse error: Expected 'EOF', got '&' at position 17: …therefore x=y ,&̲emsp;y=x-a/b \t…
最后的 x,y即为答案。
假设d=gcd(a,b),则x,y所有解:
$ x=x+(b/d)t ,y=y-(a/d)t$; 其中t为任意常整数
欧拉函数
- 在数论,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目( φ(1)=1)
通式
φ(x)=xi=1∏n(1−pi1)
其中p1, p2……pn为x的所有质因数,x是不为0的整数。
特殊性质
- 欧拉函数是积性函数——若m,n互质,则 φ(mn)=φ(m)φ(n)
- 若 n为质数,则 φ(2n)=φ(n)
- 若 n为质数,则 φ(n)=n−1
与欧拉定理、费马小定理的关系
- 任何两个互质的正整数a, m(m>=2)有
aφ(m)≡1(mod m)
即欧拉定理- 当m是质数p时,此式则为:
xp−1≡1(mod p)
即费马小定理。
代码
int Phi(int n){
int ret=1,i;
for(i=2;i*i<=n;i++){
if(n%i==0){
n/=i,ret*=i-1;
while(n%i==0) n/=i,ret*=i;
}
}
if(n>1) ret*=n-1;
return ret;
}
乘法逆元
- 若 ax≡1 mod m, 则称a关于1模m的乘法逆元为x。也可表示为 ax≡1(mod m)。
- 如果 a,m不互质,则无解。如果 m为质数,则从1到 m−1的任意数都与 m互质,即在1到 m−1之间都恰好有一个关于模 m的乘法逆元。
求法
费马小定理求逆元。
- 费马小定理: am−1≡1(mod m) (m为素数)
- 变形得: a⋅am−2≡1(mod m)
- 故 am−2为a在模m下的逆元。( am−2用快速幂求解即可)
- 注意: m必须是质数,且 a,m互质。(ACM的题一般都是模( 109+7),所以基本上都能用)
扩展欧几里德算法求逆元
- 扩展欧几里德算法:$ ax+by = gcd(a, b) $
- 令 b=m ,由于 a,m互质,所以 gcd(a,m)=1,即$ ax+my = 1 ,两边同时模m,得ax \equiv 1(mod$ m)
- 这样解出来的 x就是 a在模 m下的逆元。
- 同样,也要求 m必须是质数,且 a,m互质。
欧拉定理求逆元
- 欧拉定理: aφ(m)≡1(mod m) ( φ(m)是小于m且与m互质的数的个数。)
- 变形得: a⋅aφ(m)−1≡1(mod m)
- 故$ a^{ \varphi (m)-1} 为a在模m下的逆元。(a^{ \varphi (m)-1}$用快速幂求解即可)
- 欧拉定理实际上是费马小定理的推广。
应用
- 有时候在求 (ba)%m时,可能由于b过大而丢失精度,这时就可以求出b的逆元来变除为乘,具体如下。
- 设 x为 b模 m的逆元。
- (ba)%m⇒(ba)×1×%m⇒(ba)×b⋅x×%m⇒a⋅x%m
快速幂
- 快速幂可以大大减少运算时循环的次数。
推导过程
KaTeX parse error: Expected & or \\ or \cr or \end at position 44: …)^{n \over 2} &\̲m̲b̲o̲x̲{n为偶数}\\ a \c…
- 上述变换显然正确。
代码
int QuickPow(int x, int n) {
int ans = 1;
while (n > 0) {
if(n&1) ans*=x;
x*=x;
n/=2 ;
}
return ans;
}
如果题目要求对m取模,则
int QuickPow(int a,int b,int m)
{
int ans=1;
a%=m;
while(b>0){
if(b&1) ans=(ans*a)%m;
b/=2;
a=(a*a)%m;
}
return ans;
}
矩阵快速幂
- 加速矩阵的幂运算。
- 和快速幂的思想是一样的,需要重载一下** * **运算符。
代码
struct Mat{ //矩阵
int data[105][105],n;
Mat(){memset(data,0,sizeof(data));} //构造函数
Mat operator*(const Mat &h){ //重载'*'运算符
Mat c;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
c.data[i][j]+=data[i][k]*h.data[k][j];
return c;
}
};
Mat Mat_qpow(Mat &a,int n){//矩阵快速幂
Mat ans;ans.n=a.n;
for(int i=0;i<n;i++) ans.data[i][i]=1;
while(n){
if(n&1) ans=ans*a;
a=a*a;
n>>=1;
}
return ans;
}
斯特林公式
- 斯特林公式是一条用来取n的阶乘的近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值已经十分准确。
公式
n!≈2πn(en)n
应用
- 求 n!在十进制下的位数,暴力肯定不行,我们直接用斯特林公式求出 n!的近似值,再求以10为底近似值的对数 +1(求其他进制下的位数类似,修改底数即可)。
容斥原理
- 在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
举例
- 如果被计数的事物有A、B、C三类,那么:
A∪B∪C=A+B+C−A∩B−B∩C−C∩A+A∩B∩C- 例如求给出一个数n,求1到 n中,有多少个数不是2,5,11,13的倍数。 A,B,C,D分别是 n/2,n/5,n/11,n/13。
Lucas定理
Lucas定理是用来求 $C(n,m) mod $ p, p为素数的值。
适用领域范围:大组合数求模,n,m>p
##公式
Cnm%p=(CpnpmCn%pm%p)%p
- 然后继续对 Cpnpm使用Lucas定理,用逆元求出 Cn%pm%p。
##证明
详见百度百科:虚空传送门
判断一个组合数是奇数还是偶数
Cnk是奇数时
n&k==k
中国剩余定理
中国剩余定理又名孙子定理,是中国古代求解一次同余式组的方法。
S:⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x≡a1(mod m1)x≡a2(mod m2)x≡a3(mod m3)...x≡an(mod mn)
前提条件
m1,m2,m3...mn必须两两互质。
公式
x=(i=1∑naitiMi)modM
Mi为除 mi外其他所有 m的乘积。
ti=Mi−1为 Mi模 mi的数论倒数( ti为 Mi模 mi意义下的乘法逆元)。
Yong表
杨表(英语:Young tableau),又称杨氏矩阵。是用于组合表示理论和舒伯特演算的工具。
定义
- 杨表是由有限的方格组成。对于一个正整数,给定一个整数分拆λ(10=1+4+5),则对应一个杨表πλ (注意这是一个递降的过程,也就是说下面一行的方格数要大于等于上一行的方格数)。可以说杨表与整数分拆 λ一一对应。
- 勾长:对于杨表中的一个方格v,其勾长 hook(v) 等于同行右边的方格数加上同列上面的方格数,再加上1(也就是他自己)。
在表示理论的应用
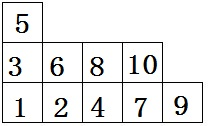
给定一个杨表 πλ ,一个有n个方格。那么把1到n这n个数字填到这个杨表中,使得每行从左到右都是递增的,每列从下到上也是递增的。用 dimπ λ 表示这样的方法个数,如图,这个这种填写数字中的一种。我们有下面的勾长公式。
勾长公式
用 dimλ表示这样的方法个数,勾长公式就是方法个数等于 n!除以所有方格的勾长的乘积。
dimπλ=∏x∈Y(λ)hook(x)n!
欧拉降幂
- 有时候幂运算指数过于庞大,我们需要先降幂再用快速幂。
- 适用范围: mod p的意义下
公式
an=⎩⎪⎨⎪⎧ab%φ(n)abab%φ(n)+φ(n)gcd(a,b)=1gcd(a,b)̸=1,b<φ(n)gcd(a,b)̸=1,b≥φ(n)
未完待续。。。