浅谈 SPFA

## 前言：

​

大家好，我是 Clare613，今天和大家好好唠一唠 SPFA。

## SPFA 算法简介：

### 何为 SPFA：

SPFA 算法是 Bellman-Ford 算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下时间复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

### 有什么用：

SPFA 作为最基础的单源最短路，个人认为类似于 BFS，代码大概是这样的：

```cpp

void SPFA(){

    memset(cnt,0x3f,sizeof(cnt));

    queue<int> q;

    q.push(s);

    cnt[s]=0;

    f[s]=1;

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:a[t]){

            if(cnt[i.v]>cnt[t]+i.w){

                cnt[i.v]=cnt[t]+i.w;

                if(!f[i.v]){

                    q.push(i.v);

                    f[i.v]=1;

                } 

            }

        }

    }

}

```

貌似对于新手不太友好，这里我们需要明确**松弛操作**。**松弛操作**是至当有一个点走到另一个点时，如果速度比原来速度快，那么就执行赋值操作，这就叫做**松弛操作**。除了**松弛操作**，就只剩下入队的问题，其实很简单，如果你在队里就不加，否则就加。

### 举个例子：

我们从 1 开始，dis 数组表示每一个点到一的当前最短距离，即之后会有所改变。队列 q 用于存储**松弛操作**的点。

#### 无向图：


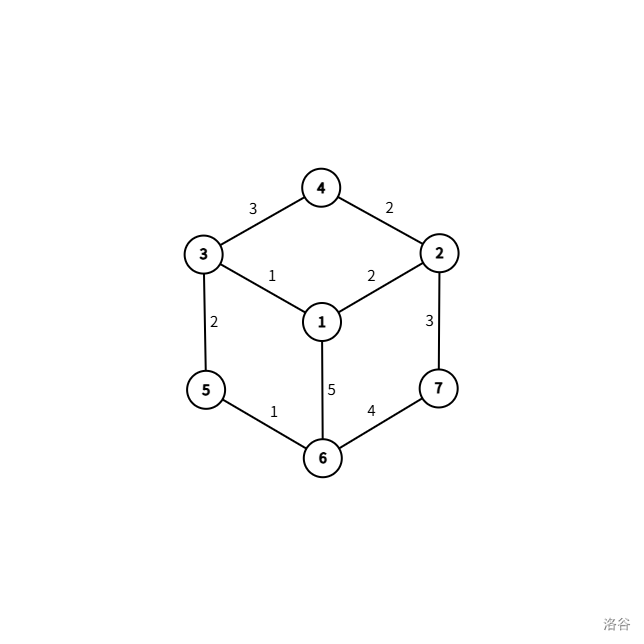
**【第零步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | INF | INF | INF | INF | INF | INF |

q:1。

_解释：最开始只有一个数 1,表示起点。_

**【第一步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | INF | INF | 5 | INF |

q:2,3,6。

_解释：q 中取出 1，将 2,3,6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第二步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | INF | 5 | 5 |

q:3,6,4,7。

_解释：q 中取出 2，可以发现 2 的 dis\_2+2 大于 dis\_1，于是不能对 1 进行__**松弛操作**__。将 4,7 的值进行__**松弛操作**__，然后将其加入队列。_

**【第三步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:6,4,7,5。

_解释：q 中取出 3，可以发现 3 的 dis\_3+1 大于 dis\_1，于是不能对 1 进行__**松弛操作**__。可以发现 3 的 dis\_3+3 等于 dis\_4，于是不必对 4 进行__**松弛操作**__。将 5 的值进行__**松弛操作**__，然后将其加入队列。_

**【第四步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:4,7,5。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第五步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:7,5。

_解释：q 中取出 4，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第六步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:5。

_解释：q 中取出 7，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第七步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:6。

_解释：q 中取出 5，可以发现 6 可以进行__**松弛操作**__。将 6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第八步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:无。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

#### 有向图：


**【第零步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | INF | INF | INF | INF | INF | INF |

q:1。

_解释：最开始只有一个数 1,表示起点。_

**【第一步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | INF | INF | 5 | INF |

q:2,3,6。

_解释：q 中取出 1，将 2,3,6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第二步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | INF | 5 | 5 |

q:3,6,4,7。

_解释：q 中取出 2。将 4,7 的值进行__**松弛操作**__，然后将其加入队列。_

**【第三步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:6,4,7,5。

_解释：q 中取出 3，可以发现 3 的 dis\_3+3 等于 dis\_4，于是不必对 4 进行__**松弛操作**__。将 5 的值进行__**松弛操作**__，然后将其加入队列。_

**【第四步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:4,7,5。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第五步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:7,5。

_解释：q 中取出 4，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第六步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:5。

_解释：q 中取出 7，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第七步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:6。

_解释：q 中取出 5，可以发现 6 可以进行__**松弛操作**__。将 6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第八步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:无。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

## 例题演练：

本期的题目均在洛谷中可以查到，分配如下：

P3371，P3385 现在讲。

P1821，P3115，P3063，P5837 为练习题。

### P3371 【模板】单源最短路径（弱化版）：

这是 SPFA 的基础题，按照前面所述的来模拟，代码放着了：

```cpp

#include<bits/stdc++.h>

using namespace std;

const int a2_31=2147483647;

struct node{

    int v,w;

};

vector<node> a[100005];

int cnt[100005],sum;

int n,m,s;

bool f[100005];

void bfs(){

    memset(cnt,0x3f,sizeof(cnt));

    queue<int> q;

    q.push(s);

    cnt[s]=0;

    f[s]=1;

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:a[t]){

            if(cnt[i.v]>cnt[t]+i.w){

                cnt[i.v]=cnt[t]+i.w;

                if(!f[i.v]){

                    q.push(i.v);

                    f[i.v]=1;

                } 

            }

        }

    }

}

int main(){

    cin>>n>>m>>s;

    for(int i=1;i<=m;i++){

        int x,y,z;

        cin>>x>>y>>z;

        a[x].push_back({y,z});

    }

    bfs();

    for(int i=1;i<=n;i++){

        if(cnt[i]>1e9) cout<<2147483647<<" ";

        else cout<<cnt[i]<<" ";

    }

    return 0;

}

```

其实没有什么可以讲的了。

### P3385 【模板】负环：

对于这道题，我们要明白，如果一个点被**松弛**了 n 次时，存在负环。为什么呢？因为每一个点最多直接或间接只能**松弛** 1 次，所以如果被**松弛**了 n 次，那么就存在负环，其他的就没有什么可以改变的了。

```cpp

#include<bits/stdc++.h>

#define int long long

using namespace std;

struct node{

    int v,w;

};

vector<node> g[2005];

int a[2005],cnt[2005];

bool f[2005];

int n,m;

string SPFA(){

    queue<int> q;

    for(int i=1;i<=n;i++) a[i]=1e9;

    memset(f,0,sizeof(f));

    memset(cnt,0,sizeof(cnt));

    a[1]=0;

    q.push(1);

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:g[t]){

            if(a[i.v]>a[t]+i.w){

                a[i.v]=a[t]+i.w;

                cnt[i.v]=cnt[t]+1;

                if(cnt[i.v]>=n) return "YES\n";

                if(!f[i.v]){

                    f[i.v]=1;

                    q.push(i.v);

                }

            }

        }

    }

    return "NO\n";

}

signed main(){

    cin.tie(0)->sync_with_stdio(0);

    int T;

    cin>>T;

    while(T--){

        cin>>n>>m;

        for(int i=1;i<=n;i++) g[i].clear();

        for(int i=1;i<=m;i++){

            int u,v,w;

            cin>>u>>v>>w;

            g[u].push_back({v,w});

            if(w>=0) g[v].push_back({u,w});

        }

        cout<<SPFA();

    }

    return 0;

}

```

快快去 A 了吧。

## 后话：

历时一个月，如果觉得好的话就请点个赞，并留言 Clyyds，谢谢。## 前言：

​

大家好，我是 Clare613，今天和大家好好唠一唠 SPFA。

## SPFA 算法简介：

### 何为 SPFA：

SPFA 算法是 Bellman-Ford 算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下时间复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

### 有什么用：

SPFA 作为最基础的单源最短路，个人认为类似于 BFS，代码大概是这样的：

```cpp

void SPFA(){

    memset(cnt,0x3f,sizeof(cnt));

    queue<int> q;

    q.push(s);

    cnt[s]=0;

    f[s]=1;

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:a[t]){

            if(cnt[i.v]>cnt[t]+i.w){

                cnt[i.v]=cnt[t]+i.w;

                if(!f[i.v]){

                    q.push(i.v);

                    f[i.v]=1;

                } 

            }

        }

    }

}

```

貌似对于新手不太友好，这里我们需要明确**松弛操作**。**松弛操作**是至当有一个点走到另一个点时，如果速度比原来速度快，那么就执行赋值操作，这就叫做**松弛操作**。除了**松弛操作**，就只剩下入队的问题，其实很简单，如果你在队里就不加，否则就加。

### 举个例子：

我们从 1 开始，dis 数组表示每一个点到一的当前最短距离，即之后会有所改变。队列 q 用于存储**松弛操作**的点。

#### 无向图：


**【第零步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | INF | INF | INF | INF | INF | INF |

q:1。

_解释：最开始只有一个数 1,表示起点。_

**【第一步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | INF | INF | 5 | INF |

q:2,3,6。

_解释：q 中取出 1，将 2,3,6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第二步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | INF | 5 | 5 |

q:3,6,4,7。

_解释：q 中取出 2，可以发现 2 的 dis\_2+2 大于 dis\_1，于是不能对 1 进行__**松弛操作**__。将 4,7 的值进行__**松弛操作**__，然后将其加入队列。_

**【第三步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:6,4,7,5。

_解释：q 中取出 3，可以发现 3 的 dis\_3+1 大于 dis\_1，于是不能对 1 进行__**松弛操作**__。可以发现 3 的 dis\_3+3 等于 dis\_4，于是不必对 4 进行__**松弛操作**__。将 5 的值进行__**松弛操作**__，然后将其加入队列。_

**【第四步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:4,7,5。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第五步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:7,5。

_解释：q 中取出 4，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第六步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:5。

_解释：q 中取出 7，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第七步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:6。

_解释：q 中取出 5，可以发现 6 可以进行__**松弛操作**__。将 6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第八步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:无。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

#### 有向图：


**【第零步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | INF | INF | INF | INF | INF | INF |

q:1。

_解释：最开始只有一个数 1,表示起点。_

**【第一步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | INF | INF | 5 | INF |

q:2,3,6。

_解释：q 中取出 1，将 2,3,6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第二步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | INF | 5 | 5 |

q:3,6,4,7。

_解释：q 中取出 2。将 4,7 的值进行__**松弛操作**__，然后将其加入队列。_

**【第三步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:6,4,7,5。

_解释：q 中取出 3，可以发现 3 的 dis\_3+3 等于 dis\_4，于是不必对 4 进行__**松弛操作**__。将 5 的值进行__**松弛操作**__，然后将其加入队列。_

**【第四步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:4,7,5。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第五步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:7,5。

_解释：q 中取出 4，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第六步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 5 | 5 |

q:5。

_解释：q 中取出 7，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

**【第七步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:6。

_解释：q 中取出 5，可以发现 6 可以进行__**松弛操作**__。将 6 的值进行__**松弛操作**__，然后将其加入队列。_

**【第八步】：**

| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|

| dis\_i | 0 | 2 | 1 | 4 | 3 | 4 | 5 |

q:无。

_解释：q 中取出 6，可以发现没有数可以进行__**松弛操作**__，直接淘汰。_

## 例题演练：

本期的题目均在洛谷中可以查到，分配如下：

P3371，P3385 现在讲。

P1821，P3115，P3063，P5837 为练习题。

### P3371 【模板】单源最短路径（弱化版）：

这是 SPFA 的基础题，按照前面所述的来模拟，代码放着了：

```cpp

#include<bits/stdc++.h>

using namespace std;

const int a2_31=2147483647;

struct node{

    int v,w;

};

vector<node> a[100005];

int cnt[100005],sum;

int n,m,s;

bool f[100005];

void bfs(){

    memset(cnt,0x3f,sizeof(cnt));

    queue<int> q;

    q.push(s);

    cnt[s]=0;

    f[s]=1;

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:a[t]){

            if(cnt[i.v]>cnt[t]+i.w){

                cnt[i.v]=cnt[t]+i.w;

                if(!f[i.v]){

                    q.push(i.v);

                    f[i.v]=1;

                } 

            }

        }

    }

}

int main(){

    cin>>n>>m>>s;

    for(int i=1;i<=m;i++){

        int x,y,z;

        cin>>x>>y>>z;

        a[x].push_back({y,z});

    }

    bfs();

    for(int i=1;i<=n;i++){

        if(cnt[i]>1e9) cout<<2147483647<<" ";

        else cout<<cnt[i]<<" ";

    }

    return 0;

}

```

其实没有什么可以讲的了。

### P3385 【模板】负环：

对于这道题，我们要明白，如果一个点被**松弛**了 n 次时，存在负环。为什么呢？因为每一个点最多直接或间接只能**松弛** 1 次，所以如果被**松弛**了 n 次，那么就存在负环，其他的就没有什么可以改变的了。

```cpp

#include<bits/stdc++.h>

#define int long long

using namespace std;

struct node{

    int v,w;

};

vector<node> g[2005];

int a[2005],cnt[2005];

bool f[2005];

int n,m;

string SPFA(){

    queue<int> q;

    for(int i=1;i<=n;i++) a[i]=1e9;

    memset(f,0,sizeof(f));

    memset(cnt,0,sizeof(cnt));

    a[1]=0;

    q.push(1);

    while(!q.empty()){

        int t=q.front();

        q.pop();

        f[t]=0;

        for(auto i:g[t]){

            if(a[i.v]>a[t]+i.w){

                a[i.v]=a[t]+i.w;

                cnt[i.v]=cnt[t]+1;

                if(cnt[i.v]>=n) return "YES\n";

                if(!f[i.v]){

                    f[i.v]=1;

                    q.push(i.v);

                }

            }

        }

    }

    return "NO\n";

}

signed main(){

    cin.tie(0)->sync_with_stdio(0);

    int T;

    cin>>T;

    while(T--){

        cin>>n>>m;

        for(int i=1;i<=n;i++) g[i].clear();

        for(int i=1;i<=m;i++){

            int u,v,w;

            cin>>u>>v>>w;

            g[u].push_back({v,w});

            if(w>=0) g[v].push_back({u,w});

        }

        cout<<SPFA();

    }

    return 0;

}

```

快快去 A 了吧。

## 后话：

历时一个月，如果觉得好的话就请点个赞，并留言 Clyyds，谢谢。