【Note】组合数学(初级)
排列组合
排列组合是组合数学中的基础。排列就是指从给定个数的元素中取出指定个数的元素进行排序;组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。在高中初等数学中,排列组合多是利用列表、枚举等方法解题。——OI-Wiki
一般思路
排列与组合组合数学的研究对象中,根据有无顺序,一般分为排列问题和组合问题。排列与组合的根本区别在于前者与元素的顺序有关,后者与元素的顺序无关。在排列与组合的问题中, 经常会出现计数问题, 解决计数问题的思路一般有以下三种:
- 只取要的。即把各种符合条件的情形枚举出来,再利用加法原理求和;
- 先全部取,再减去不要的。即把所有可能的情形枚举出来,再减去不符合条件的情形;
- 先取后排。即先把各步中符合条件的排列或组合计算出来,再根据乘法原理求积。
加法原理和乘法原理
加法原理
一道题的解法有 类,第
类有
个解法,那么这道题总共有
种不同的解法。
乘法原理
解决一道题需要 个步骤,第
个步骤有
种做法,那么这道题的解法共有
种解法。
某种样式的运动服由底色和装饰条纹的颜色配成。底色可选红、蓝、橙、黄,条纹色可选黑、白,则共有 种着色方案。若此例改成底色和条纹都用红、蓝、橙、黄四种颜色的话,此时有
种着色方案(条纹和底色不能是同一种颜色)。
在乘法法则中要注意事件 A 和 事件 B 的相互独立,以及一些隐含规则。
排列与组合基础
前置知识
表示
的阶乘,即
。特别的,
排列数
从 个不同元素中取出
个元素组成一个排列,可以组成的所有排列的个数叫做排列数,用符号
表示。
排列数的计算公式如下:
可以理解为有 个人排队,总共有
个位置,第一个位置可以从
个人里面选,第二个位置可以从
个人里面选,以此类推,第
个位置可以从
个人里面选。
全排列则是排列数的一种特殊情况,即 。其排列数为:
组合数
定义及公式
从 个不同元素中,任取
个元素组成一个集合(叫做一个组合),可以组成集合的个数叫做组合数,也被称为二项式系数。用符号
(或
)表示。
组合数的计算公式如下:
可以这样理解:从 个人中选
个人,选出
个人排列的话有
种排法。同样的
个人,组合不考虑顺序,所以只会有
种组合,但却有
种排列(相当于
个人进行全排列)。所以我们要将多出的
种排列除掉。
性质一
解释:从 个元素中选
个也就等价于从
个元素中选出
个元素排除,从而选出剩余的
个元素。
公式证明如下:
性质二
解释:我们在对 个元素中的一个做选与不选的决定后,还剩
个数。
- 如果没选它,还可以选
个数,还有
种组合;
- 如果选了它,还可以选
个数,还有
种组合。
公式证明如下:
插板法
插板法是用于求一类给相同元素分组的方案数的一种技巧,也可以用于求一类线性不定方程的解的组数。
正整数解的数目
问题一:现有 个完全相同的元素,要求将其分为
组,每组至少有一个元素,一共有多少种分法?
由于每组至少一个元素, 个元素两两之间有
个空,只需要插入
个板子,就可以分为
组。因为元素是完全相同的,所以答案就是
。
本质上是在求解方程 的正整数的个数。
非负整数解的数目
问题二:现有 个完全相同的元素,要求将其分为
组,允许组为空,一共有多少种分法?
假设我们借来 个元素,现在有
的元素,那么有
个空位,我们在其中插入
个板子,这样形成
组,并且保证了每一组不为空。此时,我们再拿出去借来的
个元素,就变成了分为
组,并且组内元素可以为空。所以答案为
.
本质上是求解 的非负整数解的组数。
不同下界整数解的数目
问题三:现有 个完全相同的元素,要求将其分为
组,第
组至少有
元素,一共有多少种分法?
本质上是求解 满足
的整数解的组数。
我们令 ,那么
这样,问题三就转化为了问题二,答案为 。
不相邻的排列
问题四:从 这
个自然数中选
个,这
个数中任何两个数都不相邻的组合有多少个?
以免我们受具体数字影响,我们将题意等价转化为:有 个球排成一排,挑选
个球并使选出的任意两个球在原来的排列中不相邻。
举个例子:若 ,答案为多少?
这个问题的解法较抽象,不容易懂,我们可以通过画图来帮助理解。
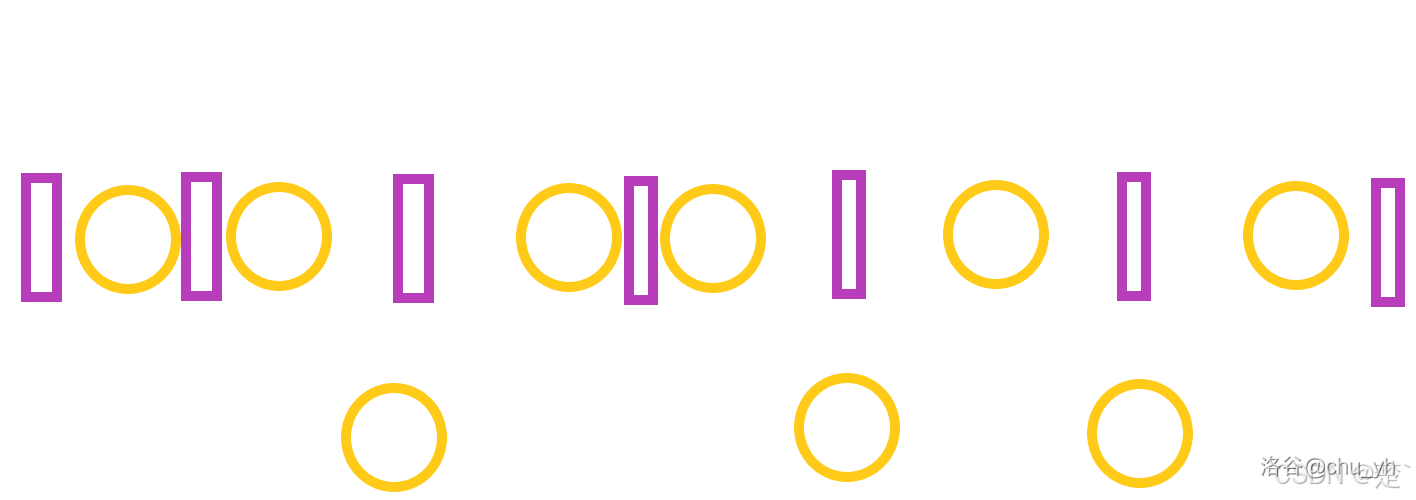 如图所示,取出
如图所示,取出 个元素,这是就产生了如紫色方框所示的
个空位

 查看12道真题和解析
查看12道真题和解析