BigDecimal 为什么可以不丢失精度？

大家好，今天咱们来聊聊 Java 中的 BigDecimal。在金融领域，数据的精确性相当重要，一个小数点的误差可能就意味着几百万甚至几千万的损失。而 BigDecimal 就是专门用来解决这种高精度计算问题的。今天，我就带大家深入了解一下，为什么 BigDecimal 能做到不丢失精度。

一、浮点数的“坑”：精度丢失

在 Java 中，我们通常用 float 或 double 来表示浮点数。但它们有一个致命的缺陷——精度丢失。比如，0.1 + 0.2 的结果并不是 0.3，而是 0.30000000000000004。这是因为在计算机内部，浮点数是用二进制表示的，而某些十进制小数无法精确地转换为二进制，从而导致了精度问题。

这种问题在金融领域是绝对不能容忍的。想象一下，银行账户余额显示为 999.999999999999，而不是 1000，用户会怎么想？所以，我们需要一种能够精确表示和计算小数的数据类型，这就是 BigDecimal 的用武之地。

二、`BigDecimal` 的“秘密武器”

BigDecimal 是 Java 中用来表示高精度小数的类，它内部使用了 BigInteger 来存储数值，并通过一个 scale 属性来记录小数点的位置。简单来说，BigDecimal 把一个小数拆成了两部分：整数部分和小数点的位置。

举个例子，2.36 在 BigDecimal 中会被表示为：

整数部分：236（用 BigInteger 存储）
小数点位置：2（表示小数点后有两位）

这样一来，BigDecimal 就可以精确地表示任何小数，而不用担心精度丢失的问题。

三、`BigDecimal` 的加法运算

我们来看一个简单的例子，理解一下 BigDecimal 是如何进行加法运算的：

BigDecimal bigDecimal1 = BigDecimal.valueOf(2.36);
BigDecimal bigDecimal2 = BigDecimal.valueOf(3.5);
BigDecimal result = bigDecimal1.add(bigDecimal2);
System.out.println(result); // 输出：5.86

在这个例子中，bigDecimal1 和 bigDecimal2 的小数位数不同（一个是两位小数，一个是两位小数）。BigDecimal 在进行加法运算时，会先将两个数的小数位数对齐，然后进行整数加法运算。

具体步骤如下：

对齐小数位数：将 3.5 转换为 3.50，这样两个数的小数位数就一致了。
整数加法：将 236 和 350 相加，得到 586。
设置小数点位置：根据小数位数（这里是两位），将结果表示为 5.86。

这个过程的核心在于，BigDecimal 把小数运算转换为了整数运算，而整数运算是不会丢失精度的。

四、`BigDecimal` 的内部实现

BigDecimal 的内部实现非常精巧。它使用了 BigInteger 来存储整数部分，这样可以保证数值的范围几乎不受限制。同时，它通过 scale 属性来记录小数点的位置，从而实现了高精度的小数运算。

我们再来看一个稍微复杂一点的例子，理解一下 BigDecimal 是如何处理不同小数位数的加法运算的：

BigDecimal bigDecimal1 = new BigDecimal("2.36");
BigDecimal bigDecimal2 = new BigDecimal("3.5");
BigDecimal result = bigDecimal1.add(bigDecimal2);
System.out.println(result); // 输出：5.86

在这个例子中，bigDecimal1 的小数位数是两位，而 bigDecimal2 的小数位数是一位。BigDecimal 在进行加法运算时，会先将两个数的小数位数对齐，然后进行整数加法运算。

具体步骤如下：

对齐小数位数：将 3.5 转换为 3.50，这样两个数的小数位数就一致了。
整数加法：将 236 和 350 相加，得到 586。
设置小数点位置：根据小数位数（这里是两位），将结果表示为 5.86。

这个过程的核心在于，BigDecimal 把小数运算转换为了整数运算，而整数运算是不会丢失精度的。

下面是add方法的源码实现：

/**
 * Returns a BigDecimal whose value is (this + augend), 
 * and whose scale is max(this.scale(), augend.scale()).
 */
public BigDecimal add(BigDecimal augend) {
    if (this.intCompact != INFLATED) {
        if ((augend.intCompact != INFLATED)) {
            return add(this.intCompact, this.scale, augend.intCompact, augend.scale);
        } else {
            return add(this.intCompact, this.scale, augend.intVal, augend.scale);
        }
    } else {
        if ((augend.intCompact != INFLATED)) {
            return add(augend.intCompact, augend.scale, this.intVal, this.scale);
        } else {
            return add(this.intVal, this.scale, augend.intVal, augend.scale);
        }
    }
}

进入第8行的add方法：

private static BigDecimal add(final long xs, int scale1, final long ys, int scale2) {
    long sdiff = (long) scale1 - scale2;
    if (sdiff == 0) {
        return add(xs, ys, scale1);
    } else if (sdiff < 0) {
        int raise = checkScale(xs,-sdiff);
        long scaledX = longMultiplyPowerTen(xs, raise);
        if (scaledX != INFLATED) {
            return add(scaledX, ys, scale2);
        } else {
            BigInteger bigsum = bigMultiplyPowerTen(xs,raise).add(ys);
            return ((xs^ys)>=0) ? // same sign test
                new BigDecimal(bigsum, INFLATED, scale2, 0)
                : valueOf(bigsum, scale2, 0);
        }
    } else {
        int raise = checkScale(ys,sdiff);
        long scaledY = longMultiplyPowerTen(ys, raise);
        if (scaledY != INFLATED) {
            return add(xs, scaledY, scale1);
        } else {
            BigInteger bigsum = bigMultiplyPowerTen(ys,raise).add(xs);
            return ((xs^ys)>=0) ?
                new BigDecimal(bigsum, INFLATED, scale1, 0)
                : valueOf(bigsum, scale1, 0);
        }
    }
}

这个例子中，该方法传入的参数分别是：xs=236，scale1=2，ys=35，scale2=1

该方法首先计算scale1 - scale2，根据差值走不同的计算逻辑，这里求出来是1，所以进入到最下面的else代码块（这块是关键）：

首先17行校验了一下数值范围
18行将ys扩大了10的n次倍，这里n=raise=1，所以返回的scaledY=350
接着就进入到20行的add方法：

private static BigDecimal add(long xs, long ys, int scale){
    long sum = add(xs, ys);
    if (sum!=INFLATED)
        return BigDecimal.valueOf(sum, scale);
    return new BigDecimal(BigInteger.valueOf(xs).add(ys), scale);
}

这个方法很简单，就是计算和，然后返回BigDecimal对象：

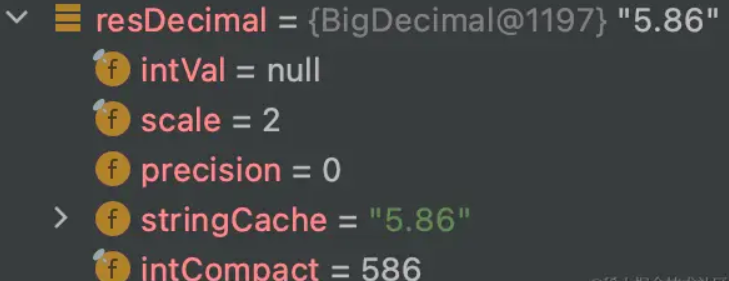
五、为什么 `BigDecimal` 不丢失精度？

现在我们已经明白了 BigDecimal 的基本原理，那么为什么它能够保证不丢失精度呢？原因就在于它把小数运算转换为了整数运算。整数运算是精确的，不会出现浮点数那种“四舍五入”的问题。

同时，BigDecimal 还提供了丰富的 API，支持各种数学运算，包括加法、减法、乘法、除法等。这些运算都基于整数运算，从而保证了精度。

举个例子，BigDecimal 的乘法运算会先将两个数的小数位数相加，然后进行整数乘法运算，最后根据总的小数位数设置小数点位置。这个过程同样保证了精度。

六、使用 `BigDecimal` 的注意事项

虽然 BigDecimal 是一个非常强大的工具，但在使用时也有一些需要注意的地方：

构造方法的选择：尽量使用字符串构造方法，而不是直接传入浮点数。因为浮点数本身就可能存在精度问题，而字符串构造方法可以精确地表示数值。
```
BigDecimal bigDecimal = new BigDecimal("2.36"); // 推荐
BigDecimal bigDecimal = BigDecimal.valueOf(2.36); // 不推荐
```
除法运算的精度：BigDecimal 的除法运算可能会出现无限循环小数的情况，所以在进行除法运算时，需要指定精度和舍入模式。
```
BigDecimal result = bigDecimal1.divide(bigDecimal2, 2, RoundingMode.HALF_UP);
```
性能问题：虽然 BigDecimal 能保证精度，但它的性能比 float 或 double 要差很多。所以在不需要高精度的场景下，尽量使用 float 或 double。