E卷-(100分)计算三叉搜索树的高度
计算三叉搜索树的高度
题目描述
K小姐正在学习数据结构,她了解到三叉搜索树的构造规则如下:
每个节点都存有一个数,当插入一个新的数时,从根节点向下寻找,直到找到一个合适的空节点插入。查找的规则是:
- 如果数小于节点的数减去
,则将数插入节点的左子树。
- 如果数大于节点的数加上
,则将数插入节点的右子树。
- 否则,将数插入节点的中子树。
现在,K小姐有一系列数,请按以上规则,按顺序将数插入树中,构建出一棵三叉搜索树,最后输出树的高度。
输入格式
第一行为一个正整数 ,表示有
个数,
。
第二行为 个空格分隔的正整数,每个数的范围为
。
输出格式
输出树的高度(根节点的高度为 )。
样例输入1
5
5000 2000 5000 8000 1800
样例输出1
3
样例解释
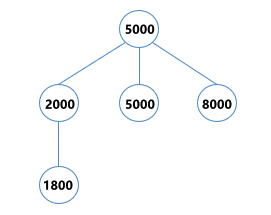
样例输入2
3
5000 4000 3000
样例输出2
3
样例解释
样例输入3
9
5000 2000 5000 8000 1800 7500 4500 1400 8100
样例输出3
4
样例解释

数据范围
每个数
题解
模拟
这道题目要求我们实现一个特殊的三叉搜索树,并计算其高度。
让我们一步步来分析这个问题:
首先,需要理解这个特殊的三叉搜索树的插入规则。
与普通的二叉搜索树不同,这里的每个节点有三个子节点:左子节点、中子节点和右子节点。插入规则基于当前节点值与待插入值之间的差值。
可以定义一个 Node 类来表示树的节点,每个节点包含一个值和三个子节点指针。
插入操作 是这个问题的核心。从根节点开始,根据插入规则递归地向下寻找合适的位置插入新节点。
在插入过程中,可以同时记录当前节点的深度。每次递归调用时,深度加一。我们用一个全局变量来记录最大深度,这就是树的高度。
-
时间复杂度分析:对于每个输入的数,我们最坏情况下需要遍历整棵树的高度。如果树是平衡的,高度约为
,其中
是节点数。所以总的时间复杂度是
。在最坏情况下(树完全不平衡),时间复杂度可能达到
。
-
空间复杂度:我们需要存储所有的节点,所以空间复杂度是
。
参考代码
- Python
class Node:
def __init__(self, val):
self.val = val # 节点的值
self.left = None # 左子节点
self.right = None # 右子节点
self.mid = None # 中子节点
def insert(root, val, depth):
global max_depth
max_depth = max(max_depth, depth) # 更新最大深度
if root is None:
return Node(val) # 如果当前节点为空,创建新节点
if val < root.val - 500:
root.left = insert(root.left, val, depth + 1) # 插入左子树
elif val > root.val + 500:
root.right = insert(root.right, val, depth + 1) # 插入右子树
else:
root.mid = insert(root.mid, val, depth + 1) # 插入中子树
return root
n = int(input()) # 读取输入的数字个数
nums = list(map(int, input().split())) # 读取所有数字
max_depth = 0 # 初始化最大深度
root = None # 初始化根节点
for num in nums:
root = insert(root, num, 1) # 插入每个数字
print(max_depth) # 输出树的高度
- C
#include <stdio.h>
#include <stdlib.h>
// 定义树节点结构
typedef struct Node {
int val;
struct Node *left, *right, *mid;
} Node;
int max_depth = 0; // 全局变量,记录最大深度
// 创建新节点
Node* newNode(int val) {
Node* node = (Node*)malloc(sizeof(Node));
node->val = val;
node->left = node->right = node->mid = NULL;
return node;
}
// 插入节点并更新最大深度
Node* insert(Node* root, int val, int depth) {
if (depth > max_depth) max_depth = depth; // 更新最大深度
if (root == NULL) return newNode(val); // 如果当前节点为空,创建新节点
if (val < root->val - 500)
root->left = insert(root->left, val, depth + 1); // 插入左子树
else if (val > root->val + 500)
root->right = insert(root->right, val, depth + 1); // 插入右子树
else
roo剩余60%内容,订阅专栏后可继续查看/也可单篇购买
本专栏收集并整理了一些刷题笔记
 查看6道真题和解析
查看6道真题和解析
 ⑨✌们拿它练练面试愣是给他整出幻觉了
⑨✌们拿它练练面试愣是给他整出幻觉了