2021牛客OI赛前集训营-普及组（第二场）解析

2021牛客OI赛前集训营-J组-2 解析

A 恰饭

题干：

牛牛来到一家餐馆恰饭。菜单里有 $4$ 道菜，价格分别为 $a_{1}, a_{2}, a_{3}, a_{4}$ 元，还有 $3$ 道甜品，价格分别为 $b_{1}, b_{2}, b_{3}$ 元。牛牛需要点一道菜和一道甜品，但牛牛又不想花费太多钱，请你帮帮他找出最小需要花费多少元。

解析：

~~这道题简直不要太难了。博主花了三个半小时零一分钟才做出来~~
额这题的话应该不用写解析了吧。直接上代码：

答案：

/*
 * @Link: https://ac.nowcoder.com/acm/contest/20101/A
 * @Date: 2021-10-06 18:33:59
 * @LastEditTime: 2021-10-06 18:37:36
 * @FilePath: \牛客\2021牛客OI赛前集训营-J\第二场\A 恰饭\eat.cpp
 * @Method: 
 */
#include <iostream>
int x = 1001, y = 1001;
int main()
{
    for (int i = 1, a; i <= 4; i++)
        scanf("%d", &a), x = a < x ? a : x;
    for (int i = 1, b; i <= 3; i++)
        scanf("%d", &b), y = b < y ? b : y;
    printf("%d", x + y);
    return 0;
}

B 卡片

题干：

牛牛有 $n$ 张卡片，第 $i$ 张卡片上有一个数字 $a_{i}$ 。牛牛在里面选出了 $k$ 张，按照某种顺序依次排列成一个数。
比如牛牛选出了 $3, 13, 1$ 这三张卡片，牛牛就可以排列成 $3131, 3113, 1331, 1313, 1133$ 这五个数。你需要帮牛牛求出对于所有选出 $k$ 张卡片的方案，牛牛总共能拼成多少种不同的数字。

解析：

显然这题要用搜索，属于比较入门的搜索题。我想学过的应该都做过类似的题吧。

答案1(AC, 6ms~9ms)：

/*
 * @Link: https://ac.nowcoder.com/acm/contest/20101/B
 * @Date: 2021-10-06 18:40:30
 * @LastEditTime: 2021-10-06 19:26:00
 * @FilePath: \牛客\2021牛客OI赛前集训营-J\第二场\B 卡片\card.cpp
 * @Method: DFS
 */
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
const int N = 19;
int n, k, card[N], cnt;
bool used[N];
vector <int> vec;
bool check(int x) // * pass
{
    for (auto i = vec.begin(); i != vec.end(); i++)
        if (*i == x)
            return true;
    return false;
}
int getDigit(int x) // * pass
{
    int ans = 0;
    while (x)
        ans++, x /= 10;
    return ans;
}
void dfs(int times, int cur)
{
    if (times == k)
    {
        // printf("%d\n", cur); //? test
        if (!check(cur))
            cnt++, vec.push_back(cur);
        return ;
    }
    for (int i = 1; i <= n; i++)
    {
        if (used[i])
            continue;
        used[i] = true;
        int temp = cur * pow(10, getDigit(card[i])) + card[i];
        // printf("%d ", temp); //? test
        dfs(times+1, temp);
        used[i] = false;
    }
}
int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
        scanf("%d", card + i);
    dfs(0, 0);
    printf("%d", cnt);
    return 0;
}

答案2(AC, 3ms~5ms, unordered_map+字符串优化)：

/*
 * @Link: https://ac.nowcoder.com/acm/contest/20101/B
 * @Date: 2021-10-06 18:40:30
 * @LastEditTime: 2021-10-07 20:50:59
 * @FilePath: \Hydro题库d:\WillCpp\牛客\2021牛客OI赛前集训营-J\第二场\B 卡片\card_AC.cpp
 * @Method: DFS
 */
#include <iostream>
#include <string>
#include <unordered_map>
std::unordered_map <std::string, bool> mp;
std::string a[17];
int cnt, n, k;
bool vis[17];
void dfs(int x, std::string s)
{
    if (x > k)
    {
        if (mp[s])
            return ;
        mp[s] = true, ++cnt;
        return ;
    }
    for (int i = 1; i <= n; i++)
    {
        if (vis[i])
            continue;
        vis[i] = true;
        dfs(x+1, s+a[i]);
        vis[i] = false;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0); std::cout.tie(0);
    std::cin >> n >> k;
    for (int i = 1; i <= n; i++)
        std::cin >> a[i];
    dfs(1, "");
    std::cout << cnt;
    return 0;
}

C 数数

题干：

我们称一个集合 $S=\{(x_1,y_1),(x_2,y_2),\ldots,(x_k,y_k)\}$ 是好的，当且仅当 $k\le 2$ 或把它们按照 $y_{i}$ 降序排序后满足：

对于所有满足 $3\le j\le$ 的 $j$ ，有 $x_{j-2} < x_j < x_{j-1}$ 或者 $x_{j-1} < x_j < x_{j-2}$ 。

牛牛在二维平面上有一个 $n$ 个点的集合。牛牛请你帮他算算有多少个非空子集 $S$ 是好的。因为答案可能很大，你只需要告诉他答案对 $1 0^{9} + 7$ 取模后的结果。

解析：

这道题属于计数问题。一般我们应对计数问题，解决办法分为三类：

枚举/搜索

通过组合数学(加法原理，乘法原理)

通过动态规划

尝试前两者后，可以发现并不好做。所以这道题我们选择用动态规划。
通过将题目中的信息作图，我们可以绘出以下两张图：

第一种合法情况：

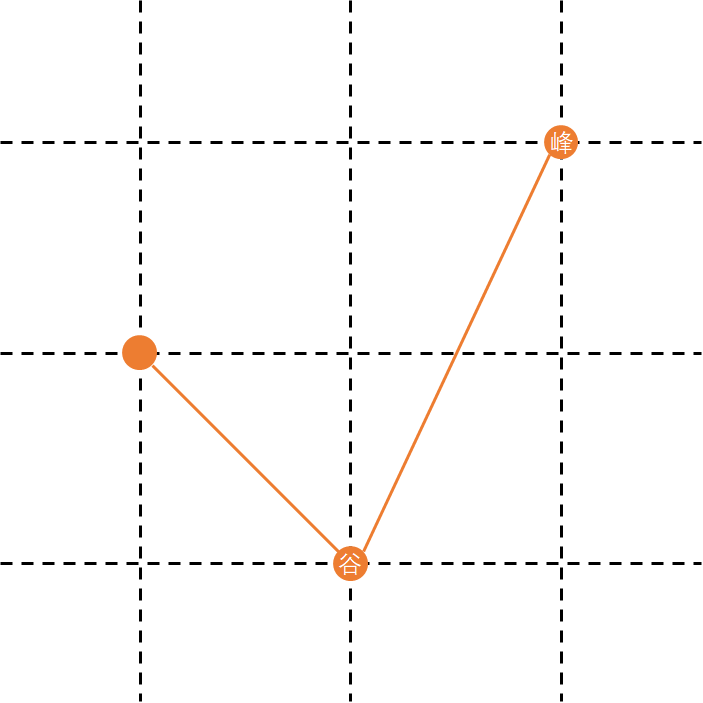
第二种合法情况：

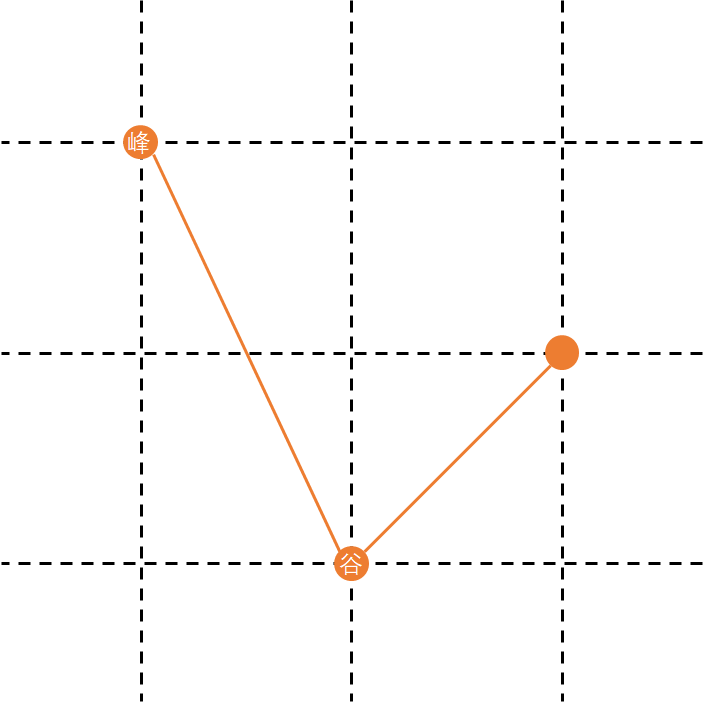
考虑动规，我们又想到两种方式：

A. 按峰谷

B. 按端点

前者的状态转移方程不太好推，所以我们选择后者。

定状态：
f[i][0] 代表 $i$ 作为右端点的所有子集 f[i][1] 代表 $i$ 作为左端点的所有子集

状态转移：

if (y[j] > y[i])
    f[j][1] += f[i][0]
else
    f[i][0] += f[j][1]

答案：

/*
 * @Link: https://ac.nowcoder.com/acm/contest/20101/C
 * @Date: 2021-10-06 19:29:06
 * @LastEditTime: 2021-10-08 21:35:35
 * @FilePath: \牛客\2021牛客OI赛前集训营-J\第二场\C 数数\count_AC.cpp
 * @Method: DP
 */
#include <iostream>
#include <algorithm>
#define x first
#define y second
const int N = 6005;
const int mod = 1e9 + 7;
std::pair <int, int> p[N];
int n, dp[N][2], ans = 0;
int main() {
    scanf("%d", &n);

    for (int i = 1; i <= n; i++)
        scanf("%d%d", &p[i].x, &p[i].y);

    std::sort(p + 1, p + n + 1);

    for (int i = 1; i <= n; i++) {
        dp[i][0] = dp[i][1] = 1;

        for (int j = i - 1; j >= 1; j--) {
            if (p[j].y > p[i].y) (dp[j][1] += dp[i][0]) %= mod;
            else (dp[i][0] += dp[j][1]) %= mod;
        }
    }

    ans = mod - n;

    for (int i = 1; i <= n; i++)
        ans = ((ans + dp[i][0]) % mod + dp[i][1]) % mod;

    printf("%d\n", ans);
    return 0;
}

D 划分

题干：

牛牛有一棵 $n$ 个节点的有根树，节点编号为 $1$ 到 $n$ ，根节点为 $1$ 。节点 $i$ 上写有数字 $a_{i}$ 。
我们称一条直链为一条 $u$ 到 $v$ 的路径，其中 $u$ 是 $v$ 的祖先或 $u = v$ （注意：这里的直链和链的定义不同）。
牛牛想要将这棵树划分成若干直链，满足每个节点恰好属于一条直链，如果对于划分出的每条直链，将该链上的点上写的数字任意排列，最后的结果满足对于任意节点 $i$ ，节点 $i$ 上写的数字为 $b_{i}$ ，那我们就称这种划分方案是好的。
你需要回答牛牛是否存在好的划分方案。

解析：

一道搜索题。dfs 搜他！

注意：

若某点的配对点不在其至根的链上 No

若某点的查找过程中遇到了别的直链 No

答案：

/*
 * @Link: https://ac.nowcoder.com/acm/contest/20101/D
 * @Date: 2021-10-07 21:27:09
 * @LastEditTime: 2021-10-08 21:44:32
 * @FilePath: \牛客\2021牛客OI赛前集训营-J\第二场\D 划分\partition_AC.cpp
 * @Method: DFS
 */
#include <iostream>
#include <cstring>
const int N = 1e5 + 9;
int t, n, m, i, j, k, a, b, bad;
int x[N], y[N], v[N], h[N], f[N];
struct Node {
    int a, b, n;
} d[N << 1];
void cun(int a, int b) {
    d[++k].a = a, d[k].b = b;
    d[k].n = h[a], h[a] = k;
}
void dfs(int a, int p) {
    int b, s, t;

    if (bad)
        return;

    for (int i = h[a]; i; i = d[i].n) {
        b = d[i].b;

        if (b == p)
            continue;

        dfs(b, f[b] = a);
    }

    if (x[a] != y[a]) {
        if (!v[a])
            v[a] = ++k;

        s = a;

        while (t = f[s]) {
            if (v[t] && v[t] != v[a])
                bad = 1;

            v[t] = v[a];

            if (x[t] == y[a]) {
                std::swap(x[t], x[a]);
                break;
            } else
                s = t;
        }

        if (!t)
            bad = 1;
    }
}
int main() {
    scanf("%d", &t);

    while (t--) {
        scanf("%d", &n);
        memset(h, 0, sizeof(h));
        memset(f, 0, sizeof(f));
        memset(v, 0, sizeof(v));

        for (i = k = 1; i < n; i++) {
            scanf("%d%d", &a, &b);
            cun(a, b);
            cun(b, a);
        }

        for (i = 1; i <= n; i++) {
            scanf("%d", &x[i]);
        }

        for (i = 1; i <= n; i++) {
            scanf("%d", &y[i]);
        }

        bad = 0;
        dfs(k = 1, 0);
        printf("%s\n", bad ? "No" : "Yes");
    }

    return 0;
}