A. Many Equal Substrings

Description:

You are given a string $t$t consisting of $n$n lowercase Latin letters and an integer number $k$k.
Let’s define a substring of some string $s$s with indices from $l$l to $r$r as $s[l\dots r]$s[l…r].
Your task is to construct such string $s$s of minimum possible length that there are exactly $k$k positions $i$i such that $s[i\dots i+n-1]=t$s[i…i+n−1]=t. In other words, your task is to construct such string $s$s of minimum possible length that there are exactly $k$k substrings of $s$s equal to $t$t.
It is guaranteed that the answer is always unique.

Input:

The first line of the input contains two integers $n$n and $k$k ( $1\le n,k\le 50$1≤n,k≤50) — the length of the string $t$t and the number of substrings.
The second line of the input contains the string $t$t consisting of exactly $n$n lowercase Latin letters.

Output

Print such string $s$s of minimum possible length that there are exactly $k$k substrings of $s$s equal to $t$t.
It is guaranteed that the answer is always unique.

Sample Input:

3 4
aba

Sample Output:

ababababa

Sample Input:

3 2
cat

Sample Output:

catcat

题目链接

用KMP中的Next数组求整个字符串的“部分匹配值”。

AC代码:

#include <bits/stdc++.h>

void GetNext(std::string str, std::vector<int> &Next) {
    int i = 0, j = -1;
    Next[0] = -1;
    int len = int(str.length());
    while (i != len) {
        if (j == -1 || str[i] == str[j]) {
            Next[++i] = ++j;
        }
        else {
            j = Next[j];
        }
    }
}

int main(int argc, char *argv[]) {
    int n, k;
    std::cin >> n >> k;
    std::string str;
    std::cin >> str;
    int len = int(str.length());
    std::vector<int> Next(len + 1, 0);
    GetNext(str, Next);
    for (int i = 0; i < Next[len]; ++i) {
        std::cout << str[i];
    }
    for (int i = 1; i <= k; ++i) {
        for (int i = Next[len]; i < len; ++i) {
            std::cout << str[i];
        }
    }
    return 0;
}

B. Creating the Contest

Description:

You are given a problemset consisting of $n$n problems. The difficulty of the $i$i-th problem is $a_i$ai​. It is guaranteed that all difficulties are distinct and are given in the increasing order.
You have to assemble the contest which consists of some problems of the given problemset. In other words, the contest you have to assemble should be a subset of problems (not necessary consecutive) of the given problemset. There is only one condition that should be satisfied: for each problem but the hardest one (the problem with the maximum difficulty) there should be a problem with the difficulty greater than the difficulty of this problem but not greater than twice the difficulty of this problem. In other words, let $a_{i_1},a_{i_2},\dots ,a_{i_p}$ai1​​,ai2​​,…,aip​​ be the difficulties of the selected problems in increasing order. Then for each $j$j from $1$1 to $p-1$p−1 $a_{i_{j+1}}\le a_{i_j}\cdot 2$aij+1​​≤aij​​⋅2 should hold. It means that the contest consisting of only one problem is always valid.
Among all contests satisfying the condition above you have to assemble one with the maximum number of problems. Your task is to find this number of problems.

Input:

The first line of the input contains one integer $n$n ( $1\le n\le 2\cdot 10^5$1≤n≤2⋅105) — the number of problems in the problemset.
The second line of the input contains $n$n integers $a_1,a_2,\dots ,a_n$a1​,a2​,…,an​ ( $1\le a_i\le 10^9$1≤ai​≤109) — difficulties of the problems. It is guaranteed that difficulties of the problems are distinct and are given in the increasing order.

Output

Print a single integer — maximum number of problems in the contest satisfying the condition in the problem statement.

Sample Input:

10
1 2 5 6 7 10 21 23 24 49

Sample Output:

4

Sample Input:

5
2 10 50 110 250

Sample Output:

1

Sample Input:

6
4 7 12 100 150 199

Sample Output:

3

题目链接

递推取最大值。

AC代码:

#include <bits/stdc++.h>

int main(int argc, char *argv[]) {
    int n;
    std::cin >> n;
    std::vector<int> a(n + 1, 0), dp(n + 1, 1);
    for (int i = 1; i <= n; ++i) {
        std::cin >> a[i];
    }
    int ans = 1;
    for (int i = 2; i <= n; ++i) {
        if (a[i] <= a[i - 1] * 2) {
            dp[i] = dp[i - 1] + 1;
        }
        ans = dp[i] > ans ? dp[i] : ans;
    }
    std::cout << ans << std::endl;
    return 0;
}

C. Maximal Intersection

Description:

You are given $n$n segments on a number line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.
The intersection of a sequence of segments is such a maximal set of points (not necesserily having integer coordinates) that each point lies within every segment from the sequence. If the resulting set isn’t empty, then it always forms some continuous segment. The length of the intersection is the length of the resulting segment or $0$0 in case the intersection is an empty set.
For example, the intersection of segments $[1;5]$[1;5] and $[3;10]$[3;10] is $[3;5]$[3;5] (length $2$2), the intersection of segments $[1;5]$[1;5] and $[5;7]$[5;7] is $[5;5]$[5;5] (length $0$0) and the intersection of segments $[1;5]$[1;5] and $[6;6]$[6;6] is an empty set (length $0$0).
Your task is to remove exactly one segment from the given sequence in such a way that the intersection of the remaining $(n-1)$(n−1) segments has the maximal possible length.

Input:

The first line contains a single integer $n$n ( $2\le n\le 3\cdot 10^5$2≤n≤3⋅105) — the number of segments in the sequence.
Each of the next $n$n lines contains two integers $l_i$li​ and $r_i$ri​ ( $0\le l_i\le r_i\le 10^9$0≤li​≤ri​≤109) — the description of the $i$i-th segment.

Output

Print a single integer — the maximal possible length of the intersection of $(n-1)$(n−1) remaining segments after you remove exactly one segment from the sequence.

Sample Input:

4
1 3
2 6
0 4
3 3

Sample Output:

1

Sample Input:

5
2 6
1 3
0 4
1 20
0 4

Sample Output:

2

Sample Input:

3
4 5
1 2
9 20

Sample Output:

0

Sample Input:

2
3 10
1 5

Sample Output:

7

题目链接

可以用multiset进行暴力查找。

AC代码:

#include <bits/stdc++.h>

int main(int argc, char *argv[]) {
    int n;
    scanf("%d", &n);
    std::vector<int> l(n), r(n);
    std::multiset<int> L, R;
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", &l[i], &r[i]);
        L.insert(l[i]);
        R.insert(r[i]);
    }
    int ans = 0;
    // 遍历枚举
    for (int i = 0; i < n; ++i) {
        // 删除此段
        L.erase(L.find(l[i]));
        R.erase(R.find(r[i]));
        ans = std::max(ans, *R.begin() - *L.rbegin());
        L.insert(l[i]);
        R.insert(r[i]);
    }
    printf("%d\n", ans);
    return 0;
}

AC代码:

#include <bits/stdc++.h>

int main(int argc, char *argv[]) {
    int n;
    scanf("%d", &n);
    std::vector<std::pair<int, int> > segs(n);
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", &segs[i].first, &segs[i].second);
    }
    sort(segs.begin(), segs.end(), [&] (const std::pair<int, int> &a, const std::pair<int, int> &b) {
        if (a.first != b.first) {
            return a.first > b.first;
        }
        return a.second < b.second;
    });
    int l = 0, r = 1e9 + 5;
    for (int i = 1; i < n; ++i) {
        l = std::max(l, segs[i].first);
        r = std::min(r, segs[i].second);
    }
    int ans = std::max(0, r - l);
    sort(segs.begin(), segs.end(), [&] (const std::pair<int, int> &a, const std::pair<int, int> &b) {
        if (a.first != b.first) {
            return a.second < b.second;
        }
        return a.first > b.first;
    });
    l = 0, r = 1e9 + 5;
    for (int i = 1; i < n; ++i) {
        l = std::max(l, segs[i].first);
        r = std::min(r, segs[i].second);
    }
    ans = std::max(ans, r - l);
    printf("%d\n", ans);
    return 0;
}

D. Concatenated Multiples

Description:

You are given an array $a$a, consisting of $n$n positive integers.
Let’s call a concatenation of numbers $x$x and $y$y the number that is obtained by writing down numbers $x$x and $y$y one right after another without changing the order. For example, a concatenation of numbers $12$12 and $3456$3456 is a number $123456$123456.
Count the number of ordered pairs of positions $(i,j)$(i,j) ( $i\ne j$i̸​=j) in array $a$a such that the concatenation of $a_i$ai​ and $a_j$aj​ is divisible by $k$k.

Input:

The first line contains two integers $n$n and $k$k ( $1\le n\le 2\cdot 10^5$1≤n≤2⋅105, $2\le k\le 10^9$2≤k≤109).
The second line contains $n$n integers $a_1,a_2,\dots ,a_n$a1​,a2​,…,an​ ( $1\le a_i\le 10^9$1≤ai​≤109).

Output

Print a single integer — the number of ordered pairs of positions $(i,j)$(i,j) ( $i\ne j$i̸​=j) in array $a$a such that the concatenation of $a_i$ai​ and $a_j$aj​ is divisible by $k$k.

Sample Input:

6 11
45 1 10 12 11 7

Sample Output:

7

Sample Input:

4 2
2 78 4 10

Sample Output:

12

Sample Input:

5 2
3 7 19 3 3

Sample Output:

0

题目链接

参考:

Codeforces Round #506 (Div. 3) D Concatenated Multiples (cf 1029D)

AC代码:

#include <bits/stdc++.h>
using namespace std;

int main(int argc, char *argv[]) {
    int n, k;
    scanf("%d%d", &n, &k);
    vector<int> a(n);
    map<int, int> mp[12];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &a[i]);
        long long x = a[i];
        for (int j = 1; j <= 10; ++j) {
            x *= 10;
            x %= k;
            mp[j][x]++;
        }
    }
    long long ans = 0;
    for (int i = 0; i < n; ++i) {
        int len = log10(a[i]) + 1;
        ans += mp[len][(k - a[i] % k) % k];
        long long x = 1;
        for (int j = 1; j <= len; ++j) {
            x = x * 10 % k;
        }
        if (((x * a[i]) % k + a[i] % k) % k == 0) {
            ans--;
        }
    }
    printf("%lld\n", ans);
    return 0;
}

E. Tree with Small Distances

Description:

You are given an undirected tree consisting of $n$n vertices. An undirected tree is a connected undirected graph with $n-1$n−1 edges.
Your task is to add the minimum number of edges in such a way that the length of the shortest path from the vertex $1$1 to any other vertex is at most $2$2. Note that you are not allowed to add loops and multiple edges.

Input:

The first line contains one integer $n$n ( $2\le n\le 2\cdot 10^5$2≤n≤2⋅105) — the number of vertices in the tree.
The following $n-1$n−1 lines contain edges: edge $i$i is given as a pair of vertices $u_i,v_i$ui​,vi​ ( $1\le u_i,v_i\le n$1≤ui​,vi​≤n). It is guaranteed that the given edges form a tree. It is guaranteed that there are no loops and multiple edges in the given edges.

Output

Print a single integer — the minimum number of edges you have to add in order to make the shortest distance from the vertex $1$1 to any other vertex at most $2$2. Note that you are not allowed to add loops and multiple edges.

Sample Input:

7
1 2
2 3
2 4
4 5
4 6
5 7

Sample Output:

2

Sample Input:

7
1 2
1 3
2 4
2 5
3 6
1 7

Sample Output:

0

Sample Input:

7
1 2
2 3
3 4
3 5
3 6
3 7

Sample Output:

1

题目链接

赛后看最短代码感觉非常巧妙！

深度优先搜索，将所有与根节点的最短距离初始化为2，递归搜索到叶子节点后不断回溯当前节点与根节点的最短距离，若其距离为2则其父节点需要和根节点相连,。

样例1：

其中递归回溯的结果即为将根节点与所有节点的父节点相连(根节点及其子节点除外)，但仅仅这么判断不完全正确。

样例:

10
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10

这个样例就不仅仅只是连接叶子节点的父节点，还需要判断中间的其它节点与根节点的最短距离。

AC代码:

#include <bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + 5;

int ans;
vector<int> tree[maxn];

int dfs(int node, int father) {
    int x = 2;
    for (int i = 0; i < int(tree[node].size()); ++i) {
        int u = tree[node][i];
        if (u != father) {
            x = min(x, dfs(u, node));
        }
    }
    // 当当前节点与父节点都不为根节点并且x=0时ans++
    if (node != 1 && father != 1 && x == 0) {
        ans++;
    }
    // 当x=2时返回0，根节点与1其父节点连线，ans++
    return (x + 1) % 3;
}

int main(int argc, char *argv[]) {
    int n;
    scanf("%d", &n);
    for (int i = 1, u, v; i < n; ++i) {
        scanf("%d%d", &u, &v);
        tree[u].push_back(v);
        tree[v].push_back(u);
    }
    ans = 0;
    dfs(1, 0);
    printf("%d\n", ans);
    return 0;
}

F. Multicolored Markers

Description:

There is an infinite board of square tiles. Initially all tiles are white.
Vova has a red marker and a blue marker. Red marker can color $a$a tiles. Blue marker can color $b$b tiles. If some tile isn’t white then you can’t use marker of any color on it. Each marker must be drained completely, so at the end there should be exactly $a$a red tiles and exactly $b$b blue tiles across the board.
Vova wants to color such a set of tiles that:
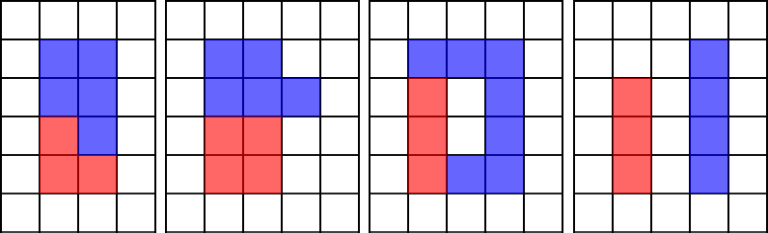
they would form a rectangle, consisting of exactly $a+b$a+b colored tiles; all tiles of at least one color would also form a rectangle.
Here are some examples of correct colorings:

Here are some examples of incorrect colorings:

Among all correct colorings Vova wants to choose the one with the minimal perimeter. What is the minimal perimeter Vova can obtain?
It is guaranteed that there exists at least one correct coloring.

Input:

A single line contains two integers $a$a and $b$b ( $1\le a,b\le 10^{14}$1≤a,b≤1014) — the number of tiles red marker should color and the number of tiles blue marker should color, respectively.

Output

Print a single integer — the minimal perimeter of a colored rectangle Vova can obtain by coloring exactly $a$a tiles red and exactly $b$b tiles blue.
It is guaranteed that there exists at least one correct coloring.

Sample Input:

4 4

Sample Output:

12

Sample Input:

3 9

Sample Output:

14

Sample Input:

9 3

Sample Output:

14

Sample Input:

3 6

Sample Output:

12

Sample Input:

506 2708

Sample Output:

3218

题目链接

直接枚举总方块能够组成矩形的边长和两种颜色分别的边长，判断是否能够存在包含关系并更新周长结果。

AC代码:

#include <bits/stdc++.h>
using namespace std;

int main(int argc, char *argv[]) {
    long long a, b;
    scanf("%lld%lld", &a, &b);
    long long mx = 1e18, ans = 1e18;
    for (long long i = 1; i * i <= (a + b); ++i) {
        // 更新a可围最大面积长边边长
        if (a % i == 0) {
            mx = min(mx, a / i);
        }
        // 更新b可围最大面积长边边长
        if (b % i == 0) {
            mx = min(mx, b / i);
        }
        // 若总数可围且能包含a、b，更新结果
        if ((a + b) % i == 0 && (a + b) / i >= mx) {
            ans = min(ans, 2 * (i + ((a + b) / i)));
        }
    }
    printf("%lld\n", ans);
    return 0;
}