【春招笔试】2025.05.08-得物春招研发岗改编题
✅ 春招备战指南 ✅
💡 学习建议:
- 先尝试独立解题(建议用时:90分钟/套)
- 对照解析查漏补缺
🧸 题面描述背景等均已深度改编,做法和题目本质基本保持一致。
🍹 感谢各位朋友们的订阅,你们的支持是我们创作的最大动力
🌸 目前本专栏已经上线60+套真题改编解析,后续会持续更新的
春秋招合集 -> 互联网必备刷题宝典🔗
题目一:螺旋迷宫蛇行挑战
1️⃣:分析螺旋路径可能的碰撞情况
2️⃣:根据路径片段长度关系,判断是否会相撞
难度:中等
这道题目的关键在于理解只能向右转的螺旋路径特性,并分析可能出现的碰撞情况。通过数学关系分析,我们可以得到判断碰撞的条件,从而实现O(n)的高效解法,避免了复杂的路径模拟。
题目二:魔法水晶共振组合
1️⃣:分析三个数两两相乘为完全平方数的数学性质
2️⃣:将每个数拆分为无平方因子部分和平方因子部分
3️⃣:统计无平方因子部分相同的数量,计算组合数
难度:中等偏难
这道题目结合了数论知识和组合计数。通过理解完全平方数的性质,发现满足条件的三元组必须具有相同的无平方因子部分。利用埃氏筛和质因数分解,可以高效地找出所有满足条件的三元组数量。
题目三:矩阵魔法变换
1️⃣:分析L形区域操作的特点和影响
2️⃣:对于足够大的矩阵,每次操作改变3个单元格的值
3️⃣:检查总和是否能被3整除或特殊情况判断
难度:中等
这道题目需要洞察矩阵操作的数学本质。关键发现是:当矩阵足够大时,每次操作影响3个单元格,因此总和必须能被3整除才可能全部变为0。对于特殊情况(如行列数小于2),需要单独判断。这种解法将复杂问题简化为简单的数学关系判断。
01. 螺旋迷宫蛇行挑战
问题描述
小基 最近开发了一款创新的迷宫游戏,在这个游戏中,玩家控制的是一条只能向右转弯的蛇形机器人。这意味着机器人的移动轨迹呈现单螺旋结构,如下图所示:
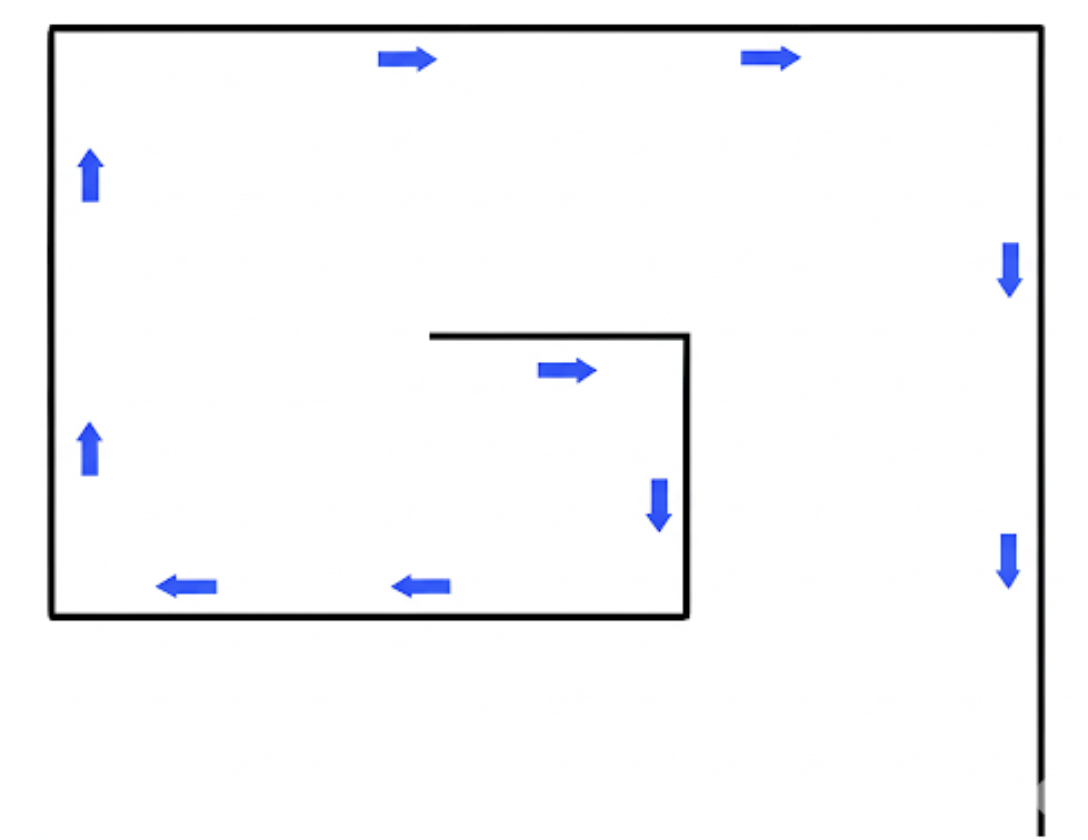
小基 将机器人的移动路径记录为一系列直线段长度,即每次直行 的长度后,右转 90 度继续前进。现在,小基 想要确定机器人是否会在移动过程中撞到自己之前的路径。
输入格式
第一行输入测试用例的个数 。
对于每一组测试用例,第一行输入机器人路径的段数 。
随后一行给出 个正整数
,表示每一段直线的长度。
输出格式
对于每一组测试用例,单独输出一行字符串。
若机器人会撞到自身路径,输出"",否则输出"
"。
样例输入
1
6
5 7 11 12 16 17
1
6
2 3 4 4 7 7
样例输出
NO
NO
数据范围
| 样例1 | 机器人按照给定的路径长度移动,不会与自己之前的路径相撞 |
| 样例2 | 机器人同样不会与自己的路径相撞 |
题解
这道题目考察的是判断一条按照特定规则移动的"蛇"是否会与自身相撞。
首先,我们需要理解题目中的单螺旋结构:机器人只能向右转弯(顺时针旋转90度),形成一个从内到外的螺旋。给定的数组表示机器人每一段直线移动的长度,之后就会右转。
判断是否相撞,本质上是检查新的移动路径是否会与之前的路径相交。对于这种螺旋形状,有几种典型的碰撞情况:
- 当前段与前前段相撞:第i段长度大于等于第(i-2)段,同时第(i-1)段长度小于等于第(i-3)段
- 当前段与更早的段相撞:需要考虑特殊的几何关系
通过分析可能的碰撞场景,我们可以得出几个判断条件:
- 如果第i段长度 >= 第(i-2)段长度,且第(i-1)段长度 <= 第(i-3)段长度,则会相撞
- 如果第(i-1)段长度等于第(i-3)段长度,且第i段长度 + 第(i-4)段长度 >= 第(i-2)段长度,则会相撞
- 还有更复杂的情况:当第(i-2)段长度 >= 第(i-4)段长度,且第i段长度 >= 第(i-2)段长度 - 第(i-4)段长度,同时第(i-1)段长度在一定范围内时,也会相撞
时间复杂度为O(N),对于给定的数据范围(N最大为10^5)完全可以接受。这种方法避免了模拟整个路径的复杂性,而是通过纯数学关系判断是否会相撞。
参考代码
- Python
import sys
input = lambda:sys.stdin.readline().strip()
def can_hit(lens):
# 判断是否会碰撞的函数
for i in range(3, len(lens)):
# 情况1: 当前段与前前段碰撞
if lens[i] >= lens[i-2] and lens[i-1] <= lens[i-3]:
return True
# 情况2: 特殊情况处理
if i >= 4 and lens[i-1] == lens[i-3] and lens[i] + lens[i-4] >= lens[i-2]:
return True
# 情况3: 更复杂的几何关系
if (i >= 5 and lens[i-2] >= lens[i-4] and
lens[i] >= lens[i-2] - lens[i-4] and
lens[i-1] >= lens[i-3] - lens[i-5] and
lens[i-1] <= lens[i-3]):
return True
return False
def main():
# 读取测试用例数
t = int(input())
for _ in range(t):
# 读取路径段数
n = int(input())
# 读取每段长度
lens = list(map(int, input().split()))
# 判断并输出结果
print("Yes" if can_hit(lens) else "NO")
if __name__ == "__main__":
main()
- Cpp
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
// 判断蛇是否会撞到自身
bool check_collision(const vector<ll>& lens) {
for (int i = 3; i < lens.size(); i++) {
// 第一种碰撞情况
if (lens[i] >= lens[i-2] && lens[i-1] <= lens[i-3]) {
return true;
}
// 第二种碰撞情况
if (i >= 4 && lens[i-1] == lens[i-3] &&
lens[i] + lens[i-4] >= lens[i-2]) {
return true;
}
// 第三种复杂碰撞情况
if (i >= 5 && lens[i-2] >= lens[i-4] &&
lens[i] >= lens[i-2] - lens[i-4] &&
lens[i-1] >= lens[i-3] - lens[i-5] &&
lens[i-1] <= lens[i-3]) {
return true;
}
}
return false;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
vector<ll> lens(n);
for (int i = 0; i < n; i++) {
cin >> lens[i];
}
bool hit = check_collision(lens);
cout << (hit ? "Yes" : "NO") << "\n";
}
return 0;
}
- Java
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine().trim());
for (int tc = 0; tc < t; tc++) {
int n = Integer.parseInt(br.readLine().trim());
String[] tokens = br.readLine().trim().split(" ");
long[] lens = new long[n];
for (int i = 0; i < n; i++) {
lens[i] = Long.parseLong(tokens[i]);
}
boolean hit = checkHit(lens);
System.out.println(hit ? "Yes" : "NO");
}
}
// 检查蛇是否会撞到自身
private static boolean checkHit(long[] lens) {
for (int i = 3; i < lens.length; i++) {
// 碰撞条件1
if (lens[i] >= lens[i-2] && lens[i-1] <= lens[i-3]) {
return true;
}
// 碰撞条件2
if (i >= 4 && lens[i-1] == lens[i-3] &&
lens[i] + lens[i-4] >= lens[i-2]) {
return true;
}
// 碰撞条件3
if (i >= 5 && lens[i-2] >= lens[i-4] &&
lens[i] >= lens[i-2] - lens[i-4] &&
lens[i-1] >= lens[i-3] - lens[i-5] &&
lens[i-1] <= lens[i-3]) {
return true;
}
}
return false;
}
}
02. 魔法水晶共振组合
问题描述
在小柯的魔法研究实验室中,有一种特殊的水晶具有奇妙的共振特性。当三块水晶的能量值分别为 、
和
时,如果它们两两结合产生的共振能量(即
、
和
)都是完美平方能量(即某个整数的平方),那么这三块水晶被称为"共振三元组"。
小柯的实验室里有编号从 到
的水晶,每块水晶的能量值等于其编号。她想知道在这些水晶中,有多少种不同的共振三元组组合,即满足
且
、
和
都是完全平方数的三元组
的数量。
输入格式
输入一个正整数 ,表示水晶的最大编号。
输出格式
输出一个整数,表示满足条件的共振三元组数量。
样例输入
9
16
样例输出
1
4
数据范围
| 样例1 | 当 |
| 样例2 | 当 |
题解
这道题目要求我们找出满足特定条件的三元组数量。条件是:三个数 、
、
两两相乘的结果都是完全平方数。
乍一看,似乎需要枚举所有可能的三元组,但这样会导致 的时间复杂度,对于
最大为
的情况来说太慢了。
仔细分析这个条件,如果 、
和
都是完全平方数,那么这三个数有什么共同特性呢?
关键洞察:如果将每个数分解为质因数的乘积,那么当两个数相乘结果为完全平方数时,意味着它们共同的质因数必须出现偶数次。
换个角度思考,我们可以将每个数表示为 ,其中
是无平方因子的部分(squarefree),
是平方因子。对于任意两个数
和
,它们的乘积是完全平方数的条件是
。
基于这个观察,我们可以计算每个 值出现的次数,然后对于每个
值,我们从对应的数中选取3个数的组合数量,即
。
算法步骤:
- 先预处理出每个数的最小质因子(使用埃氏筛法)
- 对于每个数
从
到
,计算其无平方因子部分
- 统计每个
值出现的次数
- 对于每个
值,计算
并累加到答案中
时间复杂度为 ,主要在于质因数分解的过程。空间复杂度为
,用于存储最小质因子和计数。
参考代码
- Python
import sys
input = lambda:sys.stdin.readline().strip()剩余60%内容,订阅专栏后可继续查看/也可单篇购买
互联网刷题笔试宝典,这里涵盖了市面上大部分的笔试题合集,希望助大家春秋招一臂之力
 查看12道真题和解析
查看12道真题和解析