平衡树笔记 2025.2.6
研究一个不高深的东东--平衡树!!
- 平衡树分很多种,今天学的是Splay(伸展树)--就是通过树上Splay操作让某个节点来到根的位置,但 树保持平衡(左小右大)
-
Splay 树是一棵二叉搜索树,查找某个值时满足性质:左子树任意节点的值 < 根节点的值 < 右子树任意节点的值。
-
一般维护:
1. Son[pos][2] pos节点的两个儿子编号 2. Fa[pos] pos节点的父亲编号 3.Size[pos] pos节点的子树大小(包括pos) 4.Val[pos] pos节点的权值 5.Cnt[pos] val[pos]的出现次数 6.Root 根节点 7.Sum 节点编号(每次有新节点就++)
-
旋转 (Rotate)
辅助函数
1.Get
bool Get(int u){return u==Son[Fa[u]][1];} //Son数组记录的是左右儿子 //Son[Fa[u]][1]就是u父亲的右儿子 //如果u就是右儿子 (u==Son[Fa[u]][1])的逻辑值为1 //u为左儿子 返回0 Son[][1]代表右儿子 Son[][0] 代表左儿子2.Update
void Update(int u){ Size[u]=Cnt[u];//首先是自己的出现次数包含在子树大小中 if(Son[u][1]) Size[u]+=Size[Son[u][1]];//有右儿子就+右儿子大小 if(Son[u][0]) Size[u]+=Size[Son[u][0]];//有左儿子就+左儿子大小 }- 考虑开始旋转
旋转分为两种 左旋(zig) 右旋(zag)
由于要满足平衡--左小右大
借助图片 点即为点权 左到右是将节点2旋到节点1处
上代码!
void Rotate(int u){ //Ft 父亲 Gft 父亲的父亲 int Ft=Fa[u],Gft=Fa[Ft]; //判断节点u是左子还是右子 bool Wson=Get(u); //将节点 Ft(1) 的 Wson(左儿子) 变成要旋转节点 u(2) //的另一个儿子(Wson^1) //把 4 变成 1 的左儿子 Son[Ft][Wson]=Son[u][Wson^1]; //把 4 的父亲从 2 变成 1 Fa[Son[Ft][Wson]]=Ft; // 1 变成 u(2) 的儿子 Son[u][Wson^1]=Ft; // u 成为 u 以前父亲的父亲(大雾) Fa[Ft]=u; // u 成为 u 以前父亲父亲的儿子 Fa[u]=Gft; // 当Gft不是根 将 u 变成Gft的儿子 if(Gft!=0) Son[Gft][Ft==Son[Gft][1]]=u; //结合图片理解 if(u!=0) Update(u); if(Ft!=0) Update(Ft); }
-
Splay
其实就是把一个节点旋转到根考虑三种情况
- x节点差一下就可以到达根
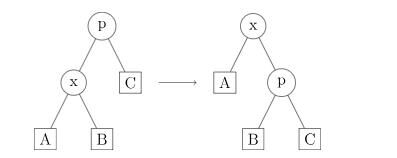
那就单旋转一次 Rotate(x)
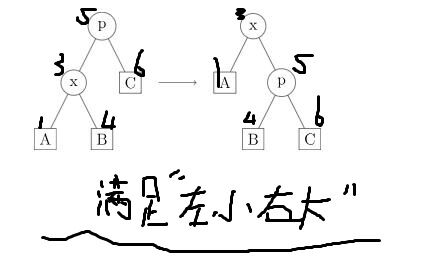
2.x节点要连续旋转两次
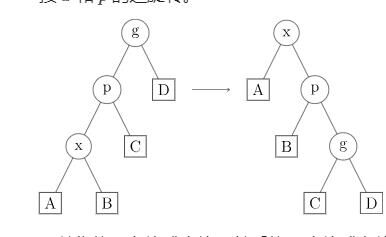
emm 那就旋转两次
3.x要一左一右旋转两次
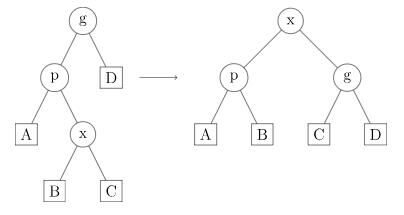
转一次x,转一次p
//Root 当前的根 int Root; //Splay 将节点u旋转至根 void Splay(int u){ //当u在Root下面,Fa[u]=0,结束循环 for(int Ft;Ft=Fa[u];Rotate(u)) if(Fa[Ft]!=0) Rotate((Get(u)==Get(Ft))?Ft:u); //双旋转 //更新根节点 Root=u; }
-
维护一个数据结构,使其可以完成
1.加入值为 x 的成员 2.删除一个值为 x 的成员 3.查询有多少数比 x 小 4.权值从小到大排名为 x 的成员 5.查询小于 x,且最大的成员的值 6.查询大于 x,且最小的成员的值一个个来
我都在讲这么久Slpay——Tree了,你说写什么?首先 Splay_Tree可以在
中完成1,2,3,4,5,6
然后Splay_Tree写起来比较简洁
所以 这里介绍Splay_Tree的写法
-
[1.加入值为 x 的成员 ]
A.
如果树空了,则直接插入根并退出。
B.
如果当前节点的权值等于 k 则增加当前节点的大小并更新节点和父亲的信息,将当前节点进行 Splay 操作
C.
否则按照二叉查找树的性质向下找,找到空节点就插入即可
//Sum 当前平衡树中有多少节点 int Sum; //插入点权为u的点 void Insert(int u){ //根为0,即当前树上没有节点 if(Root==0){ //节点数量+1 Sum++; //初始化一下 Son[Sum][0]=Son[Sum][1]=Fa[Sum]=0; //根节点就是一号节点 Root=Sum; //一号节点的子树与u值出现次数为1 Size[Sum]=Cnt[Sum]++; //给予点权 Val[Sum]=u; return ; } //找可以插入u的位置 //从根开始向下找 int Now=Root,Ft=0; for(int i=1;i>=0;i++){ //Now节点的值与u一样 if(u==Val[Now]){ //出现次数++ Cnt[Now]++; //更新 if(Now!=0) Update(Now); if(Ft!=0) Update(Ft); //将now旋转到根处 Splay(Now); break; } Ft=Now; //向下找可能的插入点 Now=Son[Now][Val[Now]<u]; //到达叶子节点 //要新开一个点 if(Now==0){ //节点编号为Sum+1 Sum++; //初始化 Son[Sum][0]=Son[Sum][1]=0; Fa[Sum]=Ft; Size[Sum]=Cnt[Sum]=1; Son[Ft][Val[Ft]<u]=Sum; Val[Sum]=u; if(Ft!=0) Update(Ft); //旋转到根 Splay(Sum); break; } } } -
[3.查询有多少数比 x 小]
A.
如果 x 比当前节点的权值小,向其左子树查找
B.
如果 x 比当前节点的权值大,将答案加上左子树(size)和当前节点(cnt)的大小,向其右子树查找
C.
如果 x 与当前节点的权值相同,将答案加 1 并返回
//找点权为u的点排名 int Find_Rank(int u){ int Now=Root,Ans=0; for(int i=1;i>=0;i++){ //如果Now点的值比u大 //向左走 if(u<Val[Now]) Now=Son[Now][0]; else{ //加上全部now的右子树的size值 Ans+=(Son[Now][0]?Size[Son[Now][0]]:0); //u点值刚刚好 //题意为Ans+1 if(u==Val[Now]){ Splay(Now); return Ans+1; } //向右儿子走 Ans+=Cnt[Now]; Now=Son[Now][1]; } } } -
[4.权值从小到大排名为 x 的成员]
A.
如果左子树非空且剩余排名 k 不大于左子树的大小 size,那么向左子树查找
B.
否则将 k 减去左子树的和根的大小。如果此时 k 的值小于等于 0,则返回根节点的权值,否则继续向右子树查找。
//找点权为u的点排名 int Find_Rank(int u){ int Now=Root,Ans=0; for(int i=1;i>=0;i++){ //如果Now点的值比u大 //向左走 if(u<Val[Now]) Now=Son[Now][0]; else{ //加上全部now的右子树的size值 Ans+=(Son[Now][0]?Size[Son[Now][0]]:0); //u点值刚刚好 //题意为Ans+1 if(u==Val[Now]){ Splay(Now); return Ans+1; } //向右儿子走 Ans+=Cnt[Now]; Now=Son[Now][1]; } } } -
[ 6.查询大于 x,且最小的成员的值]
[5.查询小于 x,且最大的成员的值 ]
其实就是查找前驱与后继
A.
前驱定义为小于 x 的最大的数,那么查询前驱可以转化为:将 x 插入(此时 x 已经在根的位置了),前驱即为 x 的左子树中最右边的节点,最后将 x 删除即可。
B.
后继定义为大于 x 的最小的数,查询方法和前驱类似:x 的右子树中最左边的节点。
int Find_From(){ int Now=Son[Root][0]; while(Son[Now][1]) Now=Son[Now][1]; return Now; } int Find_Neut(){ int Now=Son[Root][1]; while(Son[Now][0]) Now=Son[Now][0]; return Now; } -
[2.删除一个值为 x 的成员 ]
放个模板,先鸽着,有缘再更
void Delete(int u){ int Ribbish=Find_Rank(u); if(Cnt[Root]>1){ Cnt[Root]--; if(Root!=0) Update(Root); return ; } if(Son[Root][1]==Son[Root][0]&&Son[Root][0]==0){ Clear(Root); Root=0; return ; } if(Son[Root][0]==0){ int Fi_Root=Root; Root=Son[Root][1]; Fa[Root]=0; Clear(Fi_Root); return ; } if(Son[Root][1]==0){ int Fi_Root=Root; Root=Son[Root][0]; Fa[Root]=0; Clear(Fi_Root); return ; } int Left_Mau=Find_From(); int Fi_Root=Root; Splay(Left_Mau); Son[Root][1]=Son[Fi_Root][1]; Fa[Son[Fi_Root][1]]=Root; Clear(Fi_Root); if(Root!=0) Update(Root); }
emm 补充一个辅助函数
//Clear 将编号为u的点清空删除
void Clear(int u){Son[u][0]=Son[u][1]=Fa[u]=Size[u]=Cnt[u]=Val[u]=0;}
附上全部代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=3e5+110;
int Read(){
int sum=0,k=1;
char c=getchar();
while(c>'9'||c<'0'){
if(c=='-') k=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
sum=sum*10+c-48;
c=getchar();
}return sum*k;
}
int Son[M][2];
int Fa[M],Size[M],Cnt[M],Val[M];
void Clear(int u){Son[u][0]=Son[u] [1]=Fa[u]=Size[u]=Cnt[u]=Val[u]=0;}
bool Get(int u){return u==Son[Fa[u]][1];}
void Update(int u){
Size[u]=Cnt[u];
if(Son[u][1]) Size[u]+=Size[Son[u][1]];
if(Son[u][0]) Size[u]+=Size[Son[u][0]];
}
void Rotate(int u){
int Ft=Fa[u],Gft=Fa[Ft];
bool Wson=Get(u);
Son[Ft][Wson]=Son[u][1-Wson];
Fa[Son[Ft][Wson]]=Ft;
Son[u][1-Wson]=Ft;
Fa[Ft]=u;
Fa[u]=Gft;
if(Gft!=0) Son[Gft][Ft==Son[Gft][1]]=u;
if(u!=0) Update(u);
if(Ft!=0) Update(Ft);
}
int Root;
void Splay(int u){
for(int Ft;Ft=Fa[u];Rotate(u))
if(Fa[Ft]!=0) Rotate((Get(u)==Get(Ft))?Ft:u);
Root=u;
}
int Sum;
void Insert(int u){
if(Root==0){
Sum++;
Son[Sum][0]=Son[Sum][1]=Fa[Sum]=0;
Root=Sum;
Size[Sum]=Cnt[Sum]++;
Val[Sum]=u;
return ;
}
int Now=Root,Ft=0;
for(int i=1;i>=0;i++){
if(u==Val[Now]){
Cnt[Now]++;
if(Now!=0) Update(Now);
if(Ft!=0) Update(Ft);
Splay(Now);
break;
}
Ft=Now;
Now=Son[Now][Val[Now]<u];
if(Now==0){
Sum++;
Son[Sum][0]=Son[Sum][1]=0;
Fa[Sum]=Ft;
Size[Sum]=Cnt[Sum]=1;
Son[Ft][Val[Ft]<u]=Sum;
Val[Sum]=u;
if(Ft!=0) Update(Ft);
Splay(Sum);
break;
}
}
}
int Find_Num(int u){
int Now=Root;
for(int i=1;i>=0;i++){
if(Son[Now][0]&&u<=Size[Son[Now][0]])
Now=Son[Now][0];
else{
int Temp=(Son[Now][0]?Size[Son[Now][0]]:0)+Cnt[Now];
if(u<=Temp) return Val[Now];
u-=Temp;
Now=Son[Now][1];
}
}
}
int Find_Rank(int u){
int Now=Root,Ans=0;
for(int i=1;i>=0;i++){
if(u<Val[Now]) Now=Son[Now][0];
else{
Ans+=(Son[Now][0]?Size[Son[Now][0]]:0);
if(u==Val[Now]){
Splay(Now);
return Ans+1;
}
Ans+=Cnt[Now];
Now=Son[Now][1];
}
}
}
int Find_From(){
int Now=Son[Root][0];
while(Son[Now][1]) Now=Son[Now][1];
return Now;
}
int Find_Neut(){
int Now=Son[Root][1];
while(Son[Now][0]) Now=Son[Now][0];
return Now;
}
void Delete(int u){
int Ribbish=Find_Rank(u);
if(Cnt[Root]>1){
Cnt[Root]--;
if(Root!=0) Update(Root);
return ;
}
if(Son[Root][1]==Son[Root][0]&&Son[Root][0]==0){
Clear(Root);
Root=0;
return ;
}
if(Son[Root][0]==0){
int Fi_Root=Root;
Root=Son[Root][1];
Fa[Root]=0;
Clear(Fi_Root);
return ;
}
if(Son[Root][1]==0){
int Fi_Root=Root;
Root=Son[Root][0];
Fa[Root]=0;
Clear(Fi_Root);
return ;
}
int Left_Mau=Find_From();
int Fi_Root=Root;
Splay(Left_Mau);
Son[Root][1]=Son[Fi_Root][1];
Fa[Son[Fi_Root][1]]=Root;
Clear(Fi_Root);
if(Root!=0) Update(Root);
}
signed main(){
int m=Read();
for(int i=1;i<=m;i++){
int oop=Read(),u=Read();
if(oop==1){
Insert(u);
continue;
}
if(oop==2){
Delete(u);
continue;
}
if(oop==3){
Insert(u);
printf("%lld\n",Find_Rank(u));
Delete(u);
continue;
}
if(oop==4){
printf("%lld\n",Find_Num(u));
continue;
}
if(oop==5){
Insert(u);
printf("%lld\n",Val[Find_From()]);
Delete(u);
continue;
}
if(oop==6){
Insert(u);
printf("%lld\n",Val[Find_Neut()]);
Delete(u);
continue;
}
}
return 0;
}
/*
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
*/
溜溜 886~
- [ 时间复杂度证明]
-
每次操作rotate为
,由于Splay_Tree是一棵二叉树,如果有
个节点,最多有
层每次上升一层可看作
,所以Splay就是
级别
-
插入,查询,删除等操作,只有在最后才会执行Splay,也可以认为是
-
执行m次,m n同阶,总的可以认为是
4.那么每次可以认为是
然后有了Slapy,就能讲讲FHQ了
**
-
------
FHQ是一种没有旋转操作的Treap,由神犇范浩强提出的,功能比 Treap强大,无旋 treap 又称分裂合并 treap。它仅有两种核心操作, 即为分裂与合并。通过这两种操作,在很多情况下可以比旋转 treap 更 方便的实现别的操作。(支持可持久化、区间操作)
2.维护以下
用结构体;
struct Tree_Node{
int lz , rz;
}



