线性代数之——正交向量与子空间
1. 正交子空间
两个向量垂直,意味着 vTw=0。
两个子空间 V 和 W 是正交的,如果 V 中的每个向量 v 都垂直于 W 中的每个向量 w。
想象你处在一个房间里,那么地面是一个子空间 V,两面墙的交线是另一个子空间 W,这两个子空间是正交的。
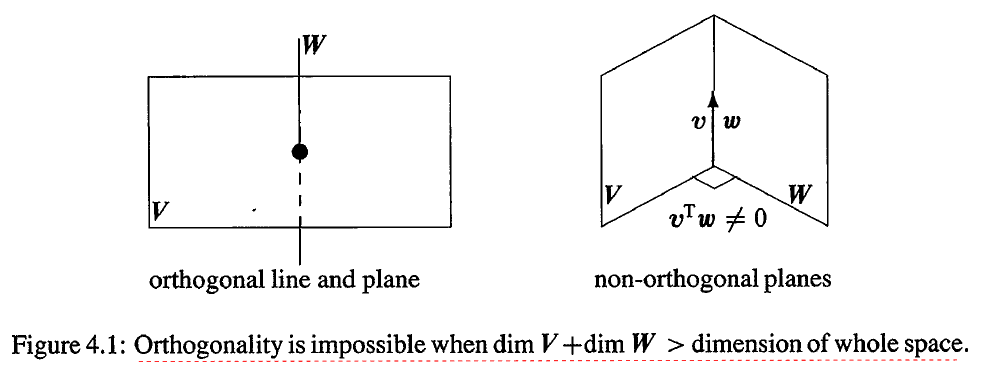
两面看起来垂直的墙不是正交的,因为它们相交于一条直线,这条直线同时存在于两个子空间,它不可能自己垂直于自己。
两个 R3 空间中的二维平面不可能正交,当两个子空间的维数之和大于整个空间的维数时,这两个子空间肯定不是正交的。
如果一个向量同时位于两个正交的子空间内,那这个向量一定是零向量,只有零向量自己垂直于自己。
零向量是零空间和行空间的唯一交点,并且零空间和行空间是 Rn 中正交的两个子空间。
由 Ax=0 可得,行空间中的每个向量和零空间中的每个向量都是垂直的,因此它们是正交的子空间。
另一方面, ATy 是对 A 的行的线性组合,那么有
xT(ATy)=(xTAT)y=(Ax)Ty=0
即,所有 A 的行的线性组合都垂直于 x。
左零空间和列空间是 Rm 中正交的两个子空间。
2. 正交补
基本空间不仅仅是正交的,它们的维数也刚刚好。行空间的维数为 r,零空间的维数为 n−r,和为 n。列空间的维数为 r,左零空间的维数为 m−r,和为 m。
R3 空间中的两条直线也可以是垂直的,但它们不可能是一个 3×3 矩阵的行空间和零空间。
一个子空间 V 的正交补(orthogonal complement)包含所有垂直于 V 的向量 ,称为 V⊥。
由这个定义,那么零空间 N(A) 是 Rn 中行空间 C(AT) 的正交补,左零空间 N(AT) 是 Rm 中列空间 C(A) 的正交补。
补的意思是说每个向量 x,都可以表示为行空间分量 xr 和零空间分量 xn 的和,那么有:
Axn=0
Axr=Ax
所有的向量都去到了列空间,乘以 A 后没有做其它的事情。
而且,任何列空间中的向量 b 都来自于行空间中的唯一一个向量。如果有 Axr=Axr′,那么 xr−xr′ 就位于零空间中,而且它也位于行空间中,所以它一定为零向量,也就是 xr=xr′。
3. 基和子空间
任何 Rn 空间中的 n 个不相关向量一定扩充出 Rn 空间,因此它们是一个基。
任何扩充出 Rn 空间的 n 个向量一定是不相关的,因此它们是一个基。
如果 A 中的 n 列是不相关的,则它们扩充出 Rn 空间,因此 Ax=b 是可解的。
如果 n 列扩充出 Rn 空间,则它们是不相关的,因此 Ax=b 有唯一解。
获取更多精彩,请关注「seniusen」!





 OPPO公司福利 630人发布
OPPO公司福利 630人发布