象棋中马的跳法

象棋问题

https://www.nowcoder.com/questionTerminal/c45704a41617402fb5c34a1778bb2645

把象棋棋盘放入第一象限,棋盘的最左下角是(0, 0)位置,那么整个棋盘就是横坐标上9条线,纵坐标上10条线的区域给你三个参数x、y、k，返回“马”从(0, 0)位置出发,必须走k步,最后落在(a,b)上的方法有多少种

暴力递归

象棋中的规则:马只能日字跳

所以下面的跳法是错的:

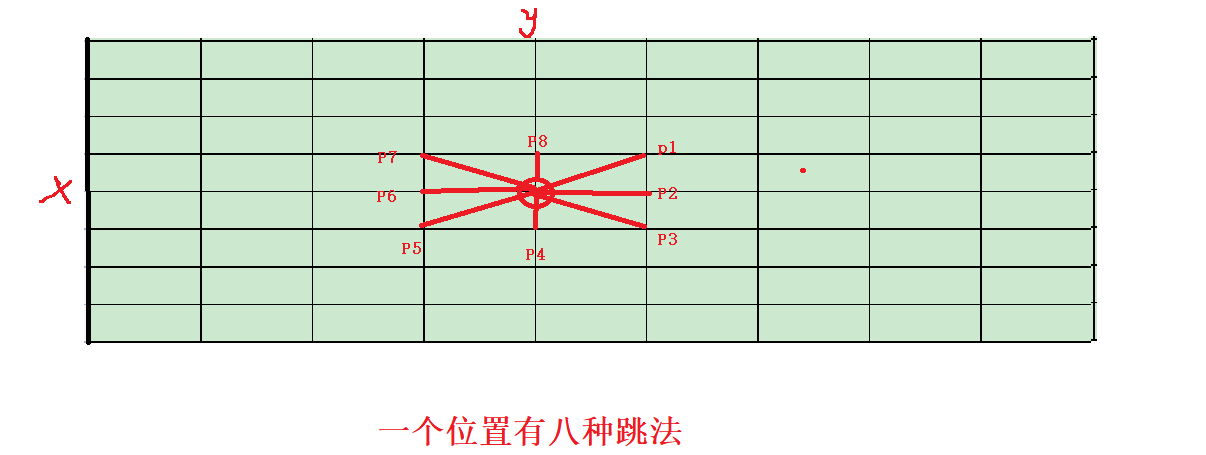
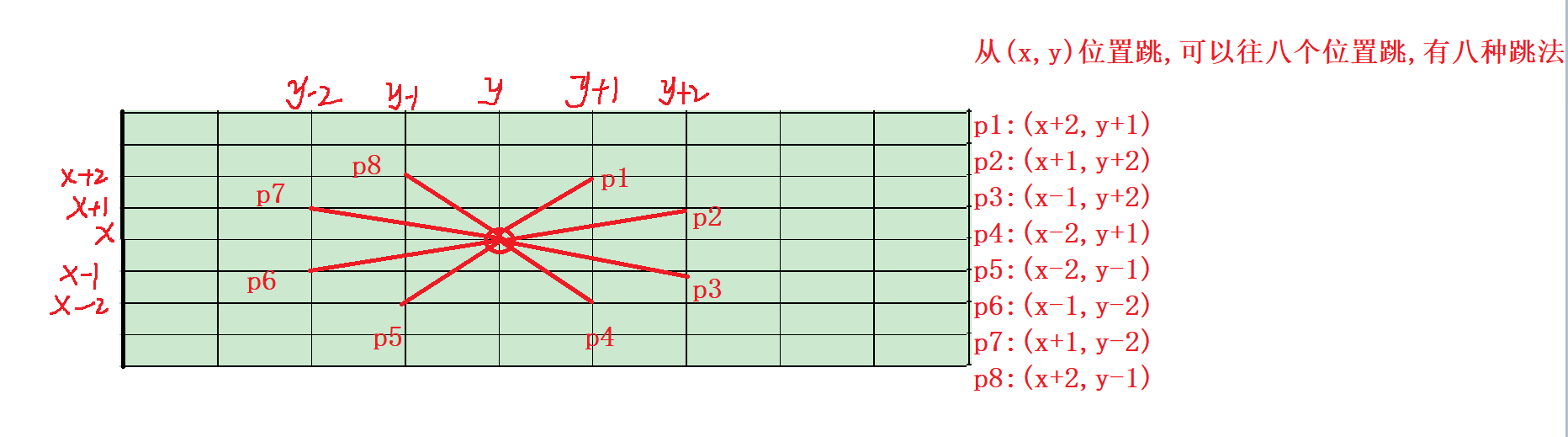
正确的跳法:

从(x,y)位置跳,可以往八个位置跳,有八种跳法

p1:(x+2,y+1) p2:(x+1,y+2) p3:(x-1,y+2) p4:(x-2,y+1)

p5:(x-2,y-1) p6:(x-1,y-2) p7:(x+1,y-2) p8:(x+2,y-1)

递归全展开,一个位置8种可能性,一共跳k步,所以暴力方法时间复杂度:O(8^k)

这八个位置分别再往后跳,最后到达(a,b)的方法数之和就是从（x，y）出发到达(a,b)的方法数

暴力方法在OJ超时！

/*
process函数的含义:
当前来到的位置是（x,y),还剩下rest步需要跳,跳完rest步之后正好跳到(a，b)的方法数是多少
*/
int process1(int x, int y, int rest, int a, int b)\
{
    //防止越界: 棋盘是10*9   
    //范围:x:0~9  y:0~8
    if (x < 0 || x > 9 || y < 0 || y > 8) {
        return 0;
    }
    //base case:剩余步数为0,如果刚好跳到了(a,b)位置就是一种方法,否则不是
    if (rest == 0) 
    {
        return (x == a && y == b) ? 1 : 0;
    }
    //从(x,y)分别往八个方向跳,剩rest-1步走, 要跳到(a,b) 的方法数 
    int ways = 0;
    ways += process1(x + 2, y + 1, rest - 1, a, b);
    ways += process1(x + 1, y + 2, rest - 1, a, b);
    ways += process1(x - 1, y + 2, rest - 1, a, b);
    ways += process1(x - 2, y + 1, rest - 1, a, b);
    ways += process1(x - 2, y - 1, rest - 1, a, b);
    ways += process1(x - 1, y - 2, rest - 1, a, b);
    ways += process1(x + 1, y - 2, rest - 1, a, b);
    ways += process1(x + 2, y - 1, rest - 1, a, b);
    return ways;
}
int jump1(int a, int b, int k)
{
    //返回从(0,0)位置开始跳,跳k步,最后跳到(a,b)的方法数
    return process1(0, 0, k,a,b);
}

int main()
{
    cout << jump1(7, 7, 10) << endl;//515813
    return 0;
}

记忆化搜索

a,b是固定参数,每次调用都不会变，而x,y,k每次调用过程都会变，因此process函数的调用结果取决于 x y k的值，我们只要用一个三维表来记录每个调用过程的返回值便能大大提高

x范围:09 y范围:08 rest的范围:0~k 所以开辟10*9*(k+1)的三维表

vector<vector<vector<int>>> dp(10, vector<vector<int>>(9, vector<int>(k + 1,-1)));

最初所以元素初始化为-1,表示每个位置都没有算过

记忆化搜索在这里OJ能过！

/*
process函数的含义:
当前来到的位置是（x,y),还剩下rest步需要跳,跳完rest步之后正好跳到(a，b)的方法数是多少
*/
int process2(int x, int y, int rest, int a, int b, vector<vector<vector<int>>>& dp)
{
    //防止越界: 棋盘是10*9   
    //范围:x:0~9  y:0~8
    if (x < 0 || x > 9 || y < 0 || y > 8) {
        return 0;
    }
    if (dp[x][y][rest] != -1)//如果值不为-1.说明之前算过这个过程,直接在表中拿值
    {
        return dp[x][y][rest];
    }
    //base case:剩余步数为0,如果刚好跳到了(a,b)位置就是一种方法,否则不是
    if (rest == 0)
    {
        int ans =  (x == a && y == b) ? 1 : 0;
        dp[x][y][rest] = ans;
        return ans;
    }
    //从(x,y)分别往八个方向跳,剩rest-1步走, 要跳到(a,b) 的方法数 
    int ways = 0;
    ways += process2(x + 2, y + 1, rest - 1, a, b, dp);
    ways += process2(x + 1, y + 2, rest - 1, a, b, dp);
    ways += process2(x - 1, y + 2, rest - 1, a, b, dp);
    ways += process2(x - 2, y + 1, rest - 1, a, b, dp);
    ways += process2(x - 2, y - 1, rest - 1, a, b, dp);
    ways += process2(x - 1, y - 2, rest - 1, a, b, dp);
    ways += process2(x + 1, y - 2, rest - 1, a, b, dp);
    ways += process2(x + 2, y - 1, rest - 1, a, b, dp);
    dp[x][y][rest] = ways;
    return ways;
}
//x范围:0~9 y范围:0~8 rest的范围:0~k
//所以开辟10*9*(k+1)的三维表
int jump2(int a, int b, int k)
{
    //返回从(0,0)位置开始跳,跳k步,最后跳到(a,b)的方法数
    vector<vector<vector<int>>> dp(10, vector<vector<int>>(9, vector<int>(k + 1,-1)));
    process2(0, 0, k, a, b,dp);
    //dp[i][j][k]的含义:从(i,j)位置,跳k步跳到目标位置(a,b)的方法数
    return dp[0][0][k];
}

严格位置依赖的动态规划

使用dp表的时间复杂度:O(10*9*K ) ->时间复杂度:O(K)

任何的rest层的东西 只依赖rest-1层,所以我们先把第0层填好,再填第一层.... 从上往下填

注意:可能存在下标越界的情况,所以封装一个函数在dp表中拿值

//为了防止下标越界,封装一个函数检测, 不越界才返回表中的值
int pick(vector<vector<vector<int>>>& dp, int x, int y, int rest)
{
    if (x < 0 || x > 9 || y < 0 || y > 8) 
    {
        return 0;
    }
    return dp[x][y][rest];
}
int jump3(int a, int b, int k)
{
    vector<vector<vector<int>>> dp(10, vector<vector<int>>(9, vector<int>(k + 1)));
    //rest=0时(第0层),只有x=a,y=b位置是1 剩下第0层的位置是0
    dp[a][b][0] = 1;
    //从第一层开始填,填到第k层
    for (int rest = 1; rest <= k; rest++) 
    {
        for (int x = 0; x < 10; x++)
        {
            for (int y = 0; y < 9; y++)
            {
                int ways = 0;
                ways += pick(dp, x + 2, y + 1, rest - 1);
                ways += pick(dp, x + 1, y + 2, rest - 1);
                ways += pick(dp, x - 1, y + 2, rest - 1);
                ways += pick(dp, x - 2, y + 1, rest - 1);
                ways += pick(dp, x - 2, y - 1, rest - 1);
                ways += pick(dp, x - 1, y - 2, rest - 1);
                ways += pick(dp, x + 1, y - 2, rest - 1);
                ways += pick(dp, x + 2, y - 1, rest - 1);
                dp[x][y][rest] = ways;
            }
        }
    }
    //dp[i][j][k]的含义:从(i,j)位置,跳k步跳到目标位置(a,b)的方法数
    //题目要求是从(0,0)出发,目标是跳k步到(a,b)
    return dp[0][0][k];
}

import java.util.*;

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int x = sc.nextInt();
        int y = sc.nextInt();
        int nums = sc.nextInt();
        int[][][] dp = new int[9][10][nums+1];
        dp[0][0][0] = 1;
        for(int i=1; i<=nums; i++){
            for(int j=0; j<9; j++){
                for(int k=0; k<10; k++){
                    dp[j][k][i] += getValue(i-1,j-1,k+2,dp);
                    dp[j][k][i] += getValue(i-1,j-2,k+1,dp);
                    dp[j][k][i] += getValue(i-1,j-2,k-1,dp);
                    dp[j][k][i] += getValue(i-1,j-1,k-2,dp);
                    dp[j][k][i] += getValue(i-1,j+1,k-2,dp);
                    dp[j][k][i] += getValue(i-1,j+2,k-1,dp);
                    dp[j][k][i] += getValue(i-1,j+2,k+1,dp);
                    dp[j][k][i] += getValue(i-1,j+1,k+2,dp);
                }
            }
        }
        System.out.println(dp[x][y][nums]);
    }
    
    public static int getValue(int l,int x,int y,int[][][] dp){
        if(x<0 || x>=9 || y<0 || y>=10){
            return 0;
        }
        return dp[x][y][l];
    }
}