回溯算法

回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。

回溯算法模板框架如下：

void backtracking(参数) {
    if(终止条件) {
        存放结果;
        return;
    }
    
    for(选择：本层集合元素(树中节点孩子的数量就是集合的大小)) {
        处理节点;
        backtracking(路径，选择列表);	//递归
        回溯，撤销处理结果
    }
}
//可以看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找到其中的一个结果了。

组合问题

给定两个整数n和k，返回1...n中所有可能的k个数的组合。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠参数startIndex，其记录了下一层递归搜索的起始位置。

LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
    backtracking(n,k,1);
    return result;
}
//每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex
public void backtracking(int n, int k, int startIndex) {
    if(path.size() == k) {
        result.add(new LinkedList(path));
        return;
    }

    //for(int i = startIndex; i <= n; i++) {      //横向遍历
    for(int i = startIndex; i <= n - (k - path.size()) + 1; i++) {//横向遍历优化  剪枝优化  省去不必要的遍历
        path.add(i);
        backtracking(n,k,i + 1);                //竖向递归 i + 1保证了元素不重复
        path.removeLast();		//回溯
    }
}

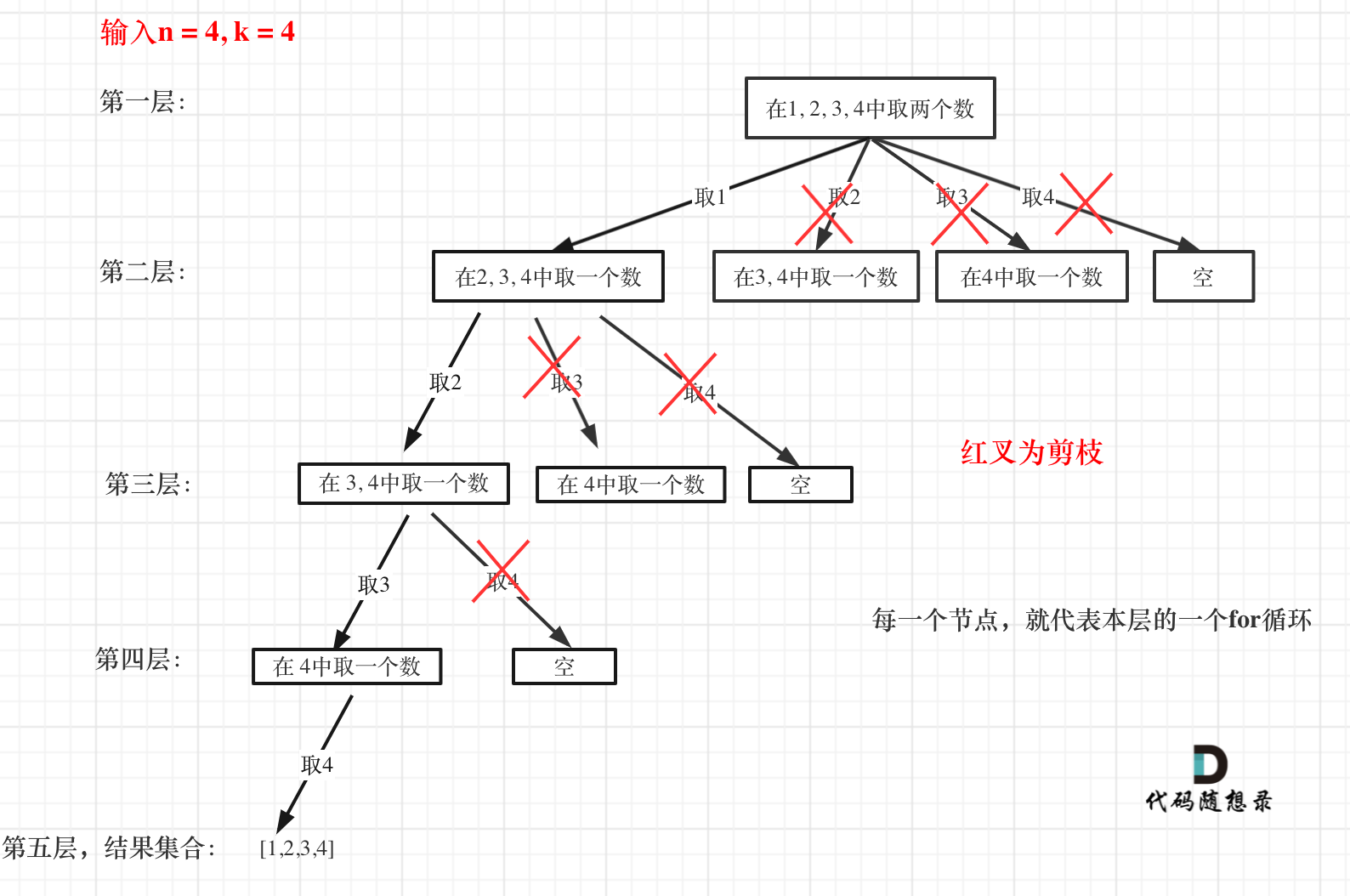
剪枝操作对应于i <= n - (k - path.size()) + 1。可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

组合总和III

找出所有相加之和为n的k个数的组合。组合中只允许含有1-9的正整数，并且每种组合中不存在重复的数字。

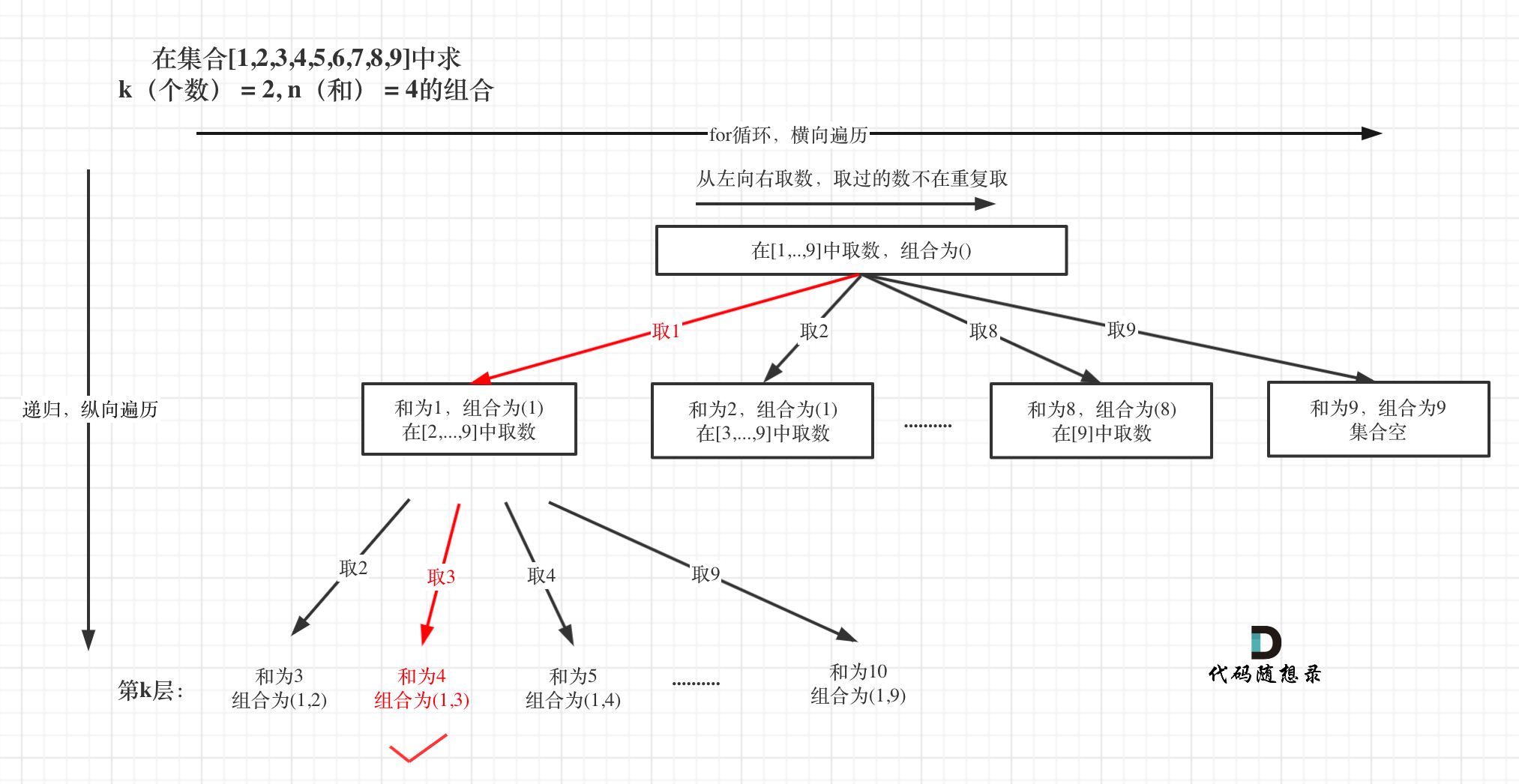
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
    backtracking(k,n,0,1);
    return result;
}

public void backtracking(int k, int target, int sum, int startIndex) {
    //剪枝操作   如果已选元素总和已经大于target了，那么往后遍历就没有意义了，直接剪掉
    if(sum > target) {
        return;
    }
    if(path.size() == k) {
        if(sum == target) {
            result.add(new LinkedList(path));
        }
        return;
    }
    //减少不必要的遍历  9 - (k - path.size()) + 1
    for(int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
        path.add(i);
        backtracking(k,target,sum + i,i + 1);       //sum + i隐藏着回溯
        path.removeLast();      //回溯
    }
}

电话号码的字母组合

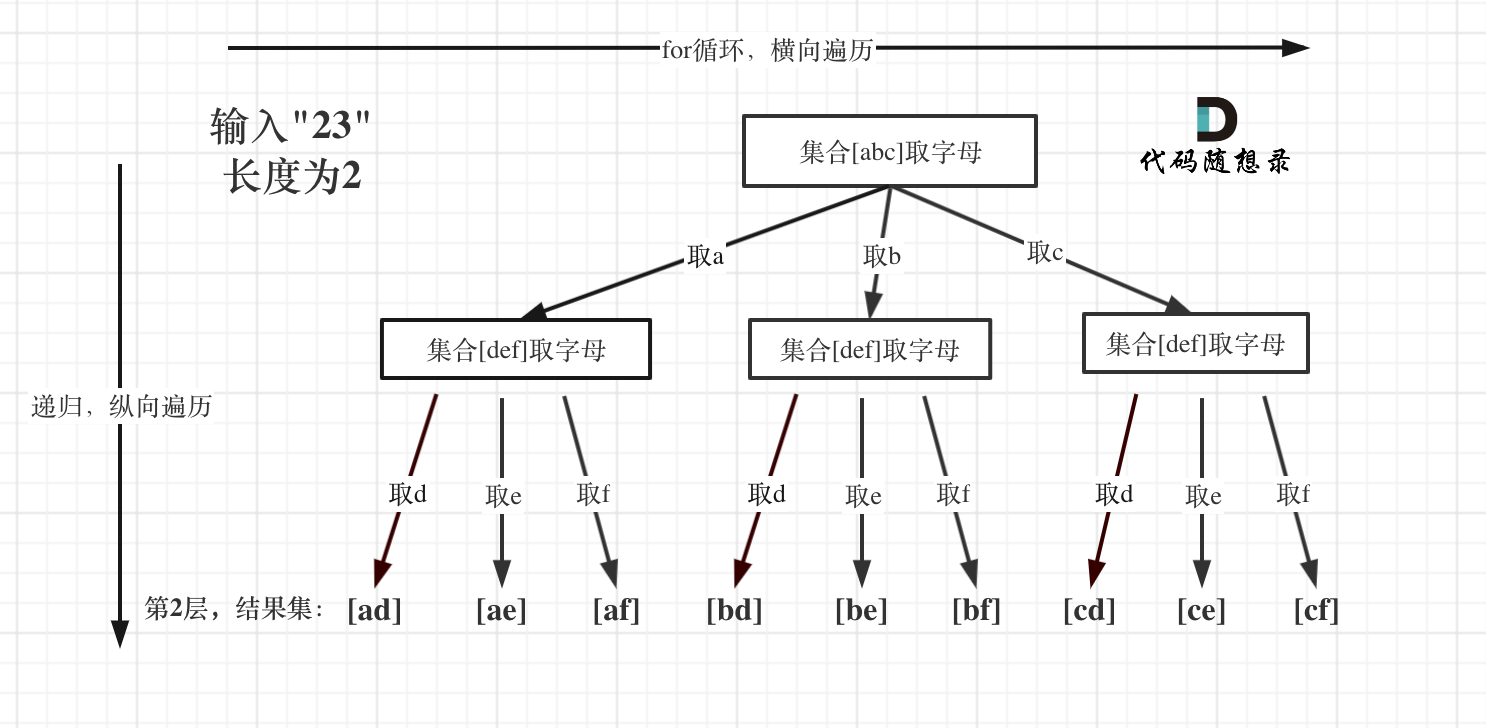
给定一个仅包含数字2-9的字符串，返回所有它能表示的字母组合。给出数字到字母的映射如下。注意1不对应任何字母。

List<String> list = new ArrayList<>();
//不同子集之间的回溯问题
public List<String> letterCombinations(String digits) {
    if(digits == null || digits.length() == 0) return list;
    //初始对应所有的数字，为了直接对应2-9，新增了两个无效的字符串""
    String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    backtracking(digits,numString,0);
    return list;
}

//每次迭代获取一个字符串，所以会涉及大量的字符串拼接，所以这里选择更为高效的StringBuilder
StringBuilder temp = new StringBuilder();

public void backtracking(String digits, String[] numString, int index) {
    if(index == digits.length()) {
        list.add(temp.toString());
        return;
    }

    String str = numString[digits.charAt(index) - '0'];
    for(int i = 0; i < str.length(); i++) {
        temp.append(str.charAt(i));
        backtracking(digits,numString,index + 1);
        //删除末尾的继续尝试  回溯
        temp.deleteCharAt(temp.length() - 1);
    }
}

注意：这里for循环不像之前的题目中从startIndex开始遍历。因为本题要求的是不同集合之间的组合，所以每次循环都应该从0开始。

组合总和

给定一个无重复元素的数组candidates和一个目标数target，找出candidates中所有可以使数字和为target的组合。

List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>(); 
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    //如果要进行优化，则必须先将candidates进行排序
    Arrays.sort(candidates);
    backtracking(candidates,target,0,0);
    return result;
}

public void backtracking(int[] candidates,int target,int sum,int startIndex) {
    if(sum == target) {
        result.add(new ArrayList<>(path));
        return;
    }
    // if(sum > target) {  优化后此处可以省略  因为大于target的sum已经不会再进入递归遍历了
    //     return;
    // }
    //优化对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历
    for(int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
        path.add(candidates[i]);
        backtracking(candidates,target,sum + candidates[i],i); //不用i+1了，表示可以重复读取当前的数
        path.remove(path.size() - 1);       //回溯
    }
}

如果是一个集合来求组合的话，就需要startIndex。如果是多个集合去组合的话，各个集合之间相互不影响，那么就不用startIndex。

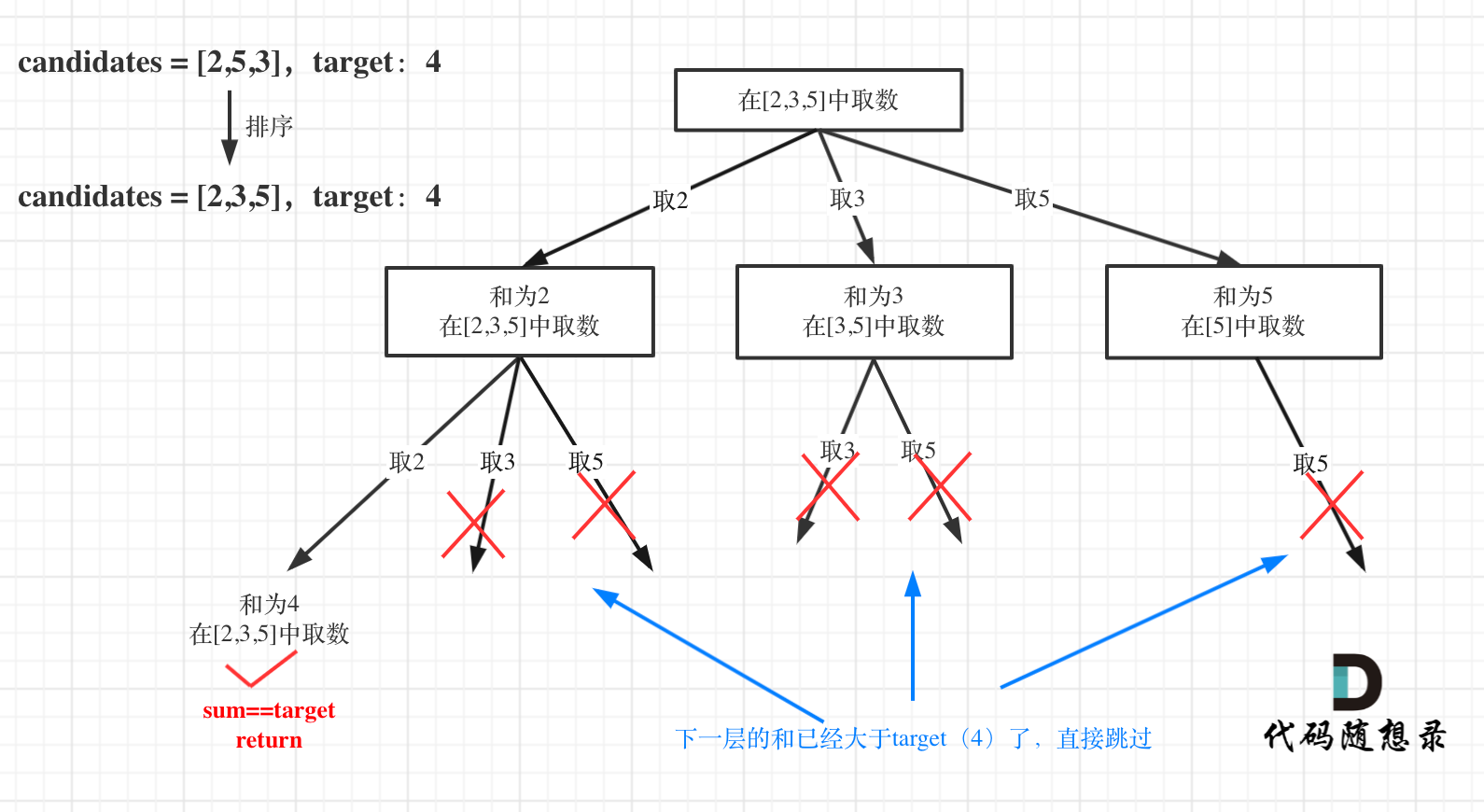
优化：对总集合排序之后（一定得排序后才能进行此优化，如果下一层的sum（就是本层的sum + candidates[i]）已经大于target，就可以结束本来for循环的遍历）。

组合总和II

给定一个数组candidates和一个目标数target，找出candidates中所有可以使数字和为target的组合。candidates中的每个数字在每个数组中只能使用一次。说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

本题与上一题的区别在于：

1. 本题candidates中的每个数字在每个组合中只能使用一次。
2. 本题数组candidates的元素是有重复的，且解集不能包含重复的组合。即元素在同一个组合内是可以重复的，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。强调一下，树层去重的话，需要对数组排序！

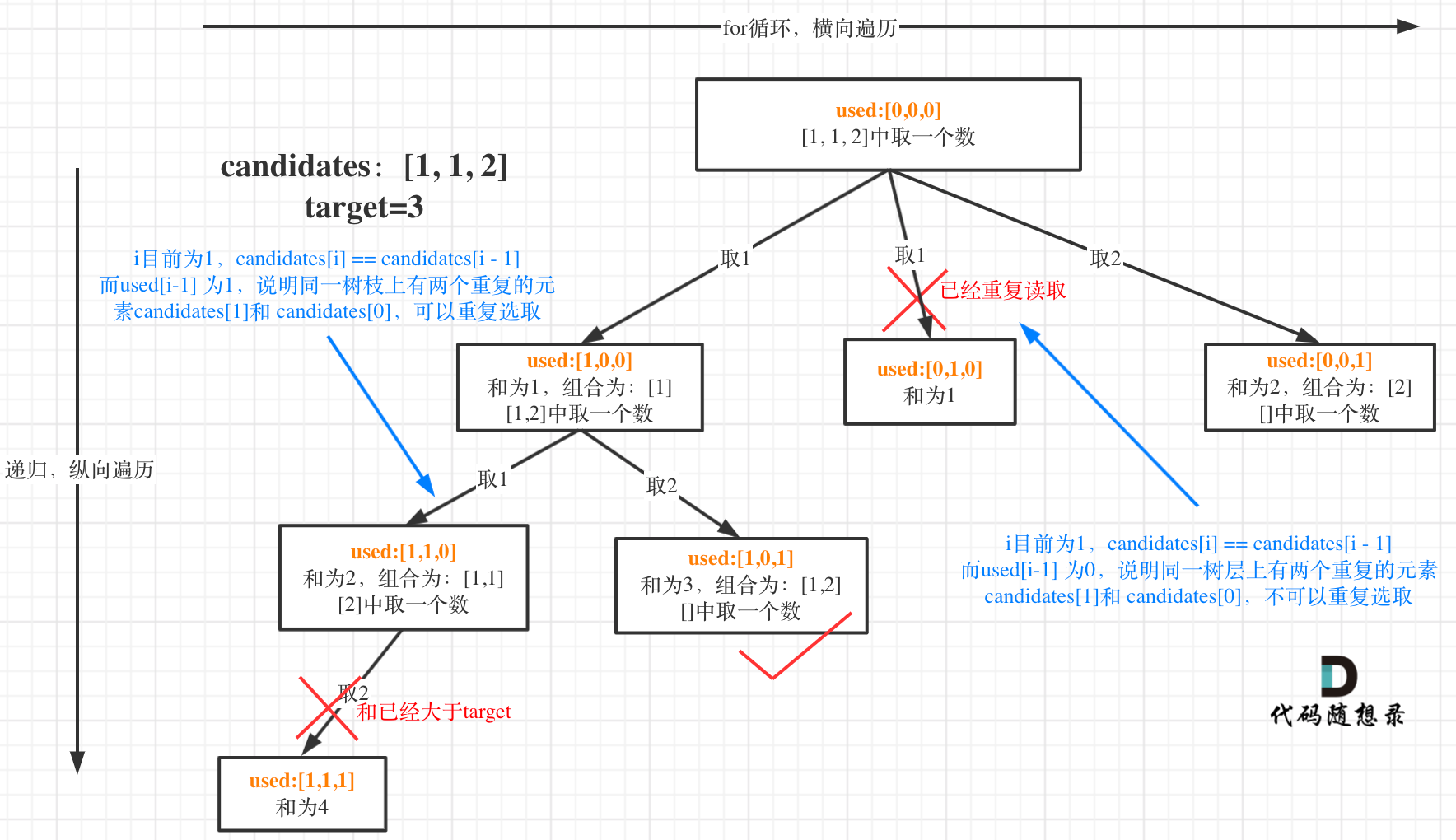
如果candidates[i] == candidates[i - 1]并且used[i - 1] == false;说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    //为了将重复的数字都放到一起，所以先进行排序
    Arrays.sort(candidates);
    //加标志数组，用来辅助判断同层节点是否已经遍历
    boolean[] flag = new boolean[candidates.length];
    int sum = 0;    //累加变量
    backTracking(candidates,target,0,sum,flag);
    return result;
}

public void backTracking(int[] candidates,int target,int startIndex,int sum,boolean[] flag) {
    if(sum == target) {
        result.add(new ArrayList<>(path));
        return;
    }

    for(int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
        //出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
        if(i > 0 && candidates[i] == candidates[i - 1] && flag[i - 1] == false) {
            continue;
        }
        //可以直接使用startIndex去重，竖向的重复不会跳过，横向的重复会跳过i = startIndex的时候就是允许竖向重复  当i>startIndex的时候,&&后半部分的条件就会被判断，若相等则跳过横向重复
        /*if (i > startIndex && candidates[i] == candidates[i - 1]) {
                continue;
            }*/

        flag[i] = true;
        path.add(candidates[i]);
        backTracking(candidates,target,i + 1,sum + candidates[i],flag); //每个节点只能使用一次，所以startIndex为i+1
        flag[i] = false;    //回溯      sum和startIndex在递归参数内进行回溯
        path.remove(path.size() - 1);   //回溯

    }
}

分割回文串

给定一个字符串s，将s分割成一些子串，使每个子串都是回文串。返回所有可能的分割方案。

List<String> path = new ArrayList<>();
List<List<String>> result = new ArrayList<>();
public List<List<String>> partition(String s) {
    backTracking(s,0);
    return result;
}

public void backTracking(String s, int startIndex) {
    //如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
    if(startIndex >= s.length()) {
        result.add(new ArrayList<>(path));
        return;
    }

    for(int i = startIndex; i < s.length(); i++) {
        if(ispalindrome(s,startIndex,i)) {   //判断是否是回文串
            String str = s.substring(startIndex, i + 1);    //获取[startIndex,i]在s中的子串
            path.add(str);
        } else {
            continue;   //不是回文串，跳过
        }
        backTracking(s,i + 1);  //寻找i+1为起始位置的子串
        path.remove(path.size() - 1);   //回溯
    }
}
//双指针法判断是否为回文串
public boolean ispalindrome(String s,int start, int end) {
    for(int i = start,j = end; i < j; i++,j--) {
        if(s.charAt(i) != s.charAt(j)) {
            return false;
        }
    }
    return true;
}

复原IP地址

给定一个只包含数字的字符串，复原它并返回所有可能的IP地址格式。有效的IP地址正好由四个整数（每个整数位于0到255之间组成，且不能含有前导0），整数之间用'.'分隔

List<String> result = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
    if(s.length() > 12) return result;
    backTracking(s,0,0);
    return result;
}

//startIndex：搜索的起始位置  pointNum：添加逗点的数量
public void backTracking(String s, int startIndex, int pointNum) {
    if(pointNum == 3) {     //逗点数量为3时，分隔结束
        //判断第四段子字符串是否合法，如果合法就放进result中
        if(isValid(s,startIndex,s.length() - 1)) {
            result.add(s);
        }
        return;
    }

    for(int i = startIndex; i < s.length(); i++) {
        if(isValid(s,startIndex,i)) {
            s = s.substring(0,i + 1) + "." + s.substring(i + 1);    //插入逗号
            backTracking(s,i + 2,pointNum + 1);     //插入逗号之后，下一个子串的初始位置为i+2
            s = s.substring(0,i + 1) + s.substring(i + 2);  //回溯删除掉逗号
        }else {
            break;
        }
    }
}

//判断字符串s在左闭右闭区间[start,end]所组成的数字是否合法
public boolean isValid(String s, int start, int end) {
    if(start > end) return false;
    //0开头的数字不合法
    if(s.charAt(start) == '0' && start != end) return false;
    int num = 0;
    for(int i = start; i <= end;i++) {
        if(s.charAt(i) > '9' || s.charAt(i) < '0') {
            return false;
        }
        num = num * 10 + (s.charAt(i) - '0');
        if(num > 255) return false;     //如果大于255则不合法
    }
    return true;
}

子集

给定一组不含重复元素的整数数组nums，返回该数组所有可能的子集。解集不能包含重复的子集。

如果把子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点。

从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合。

List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
    backTracking(nums,0);
    return result;
}
//子集问题是收集树形结构中所有节点的结果。
public void backTracking(int[] nums,int startIndex) {
    result.add(new ArrayList<>(path));      //收集子集，要放在终止添加的上面，否则会漏掉自己
    if(startIndex >= nums.length) return;   //此处终止条件可以不加，因为满足此终止条件时，下面for循环也不会进入，则会自动退出本轮递归，相当于终止。

    for(int i = startIndex; i < nums.length; i++) {
        path.add(nums[i]);
        backTracking(nums,i + 1);
        path.remove(path.size() - 1);
    }
}

求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

子集II

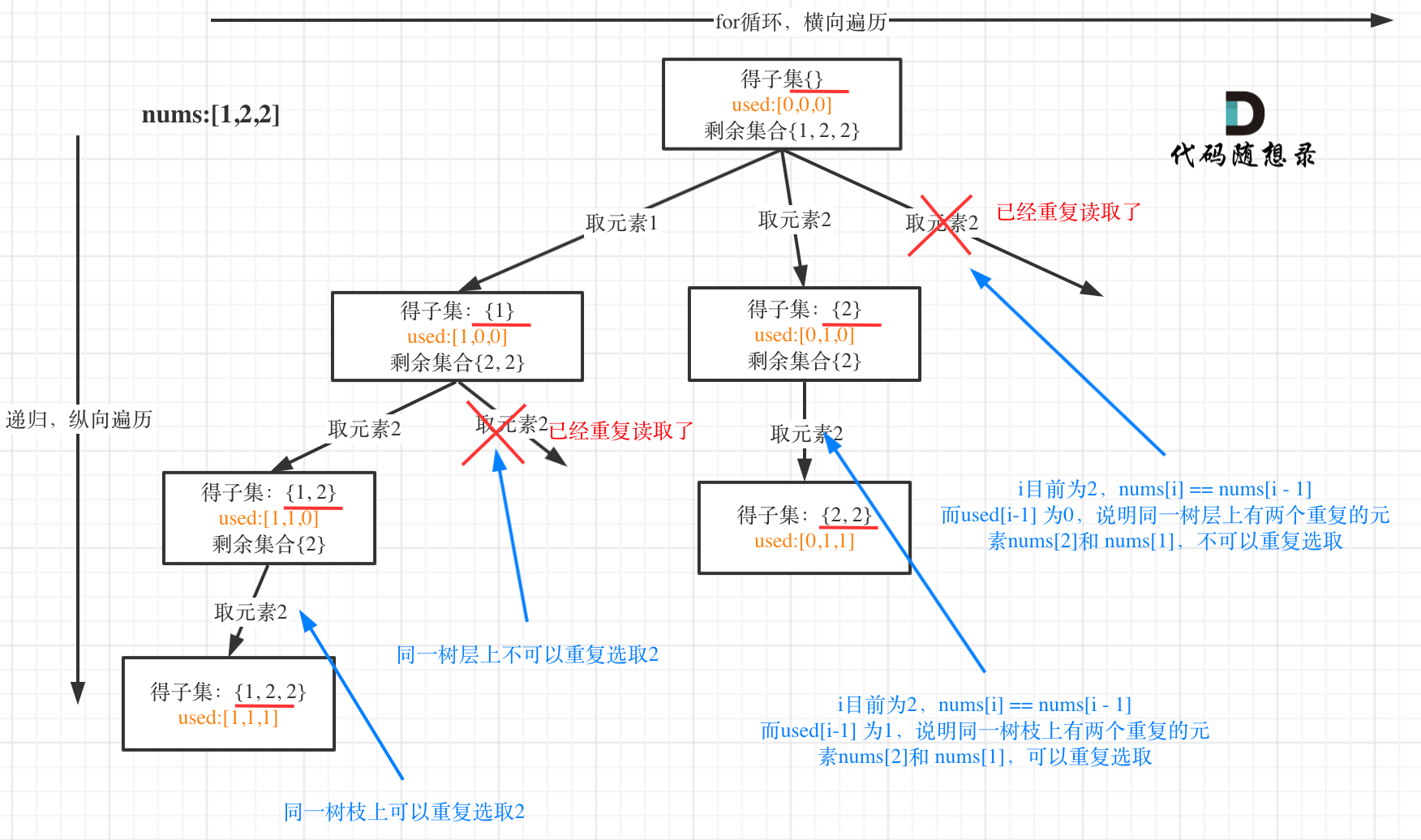
给定一个可能包含重复元素的整数数组nums，返回该数组所有可能的子集。说明：解集不能包含重复的子集。

List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
    boolean[] flag = new boolean[nums.length];
    Arrays.sort(nums);      //要实现去重，应该先将数组进行排序
    backTracking(nums,0,flag);
    return result;
}

public void backTracking(int[] nums,int startIndex,boolean[] flag) {
    result.add(new ArrayList<>(path));

    if(startIndex >= nums.length) return;

    for(int i = startIndex; i < nums.length; i++) {
        if(i > 0 && nums[i] == nums[i - 1] && flag[i - 1] == false) {
            continue;
        }
        path.add(nums[i]);
        flag[i] = true;
        backTracking(nums,i + 1,flag);
        flag[i] = false;
        path.remove(path.size() - 1);
    }
}

递增子序列

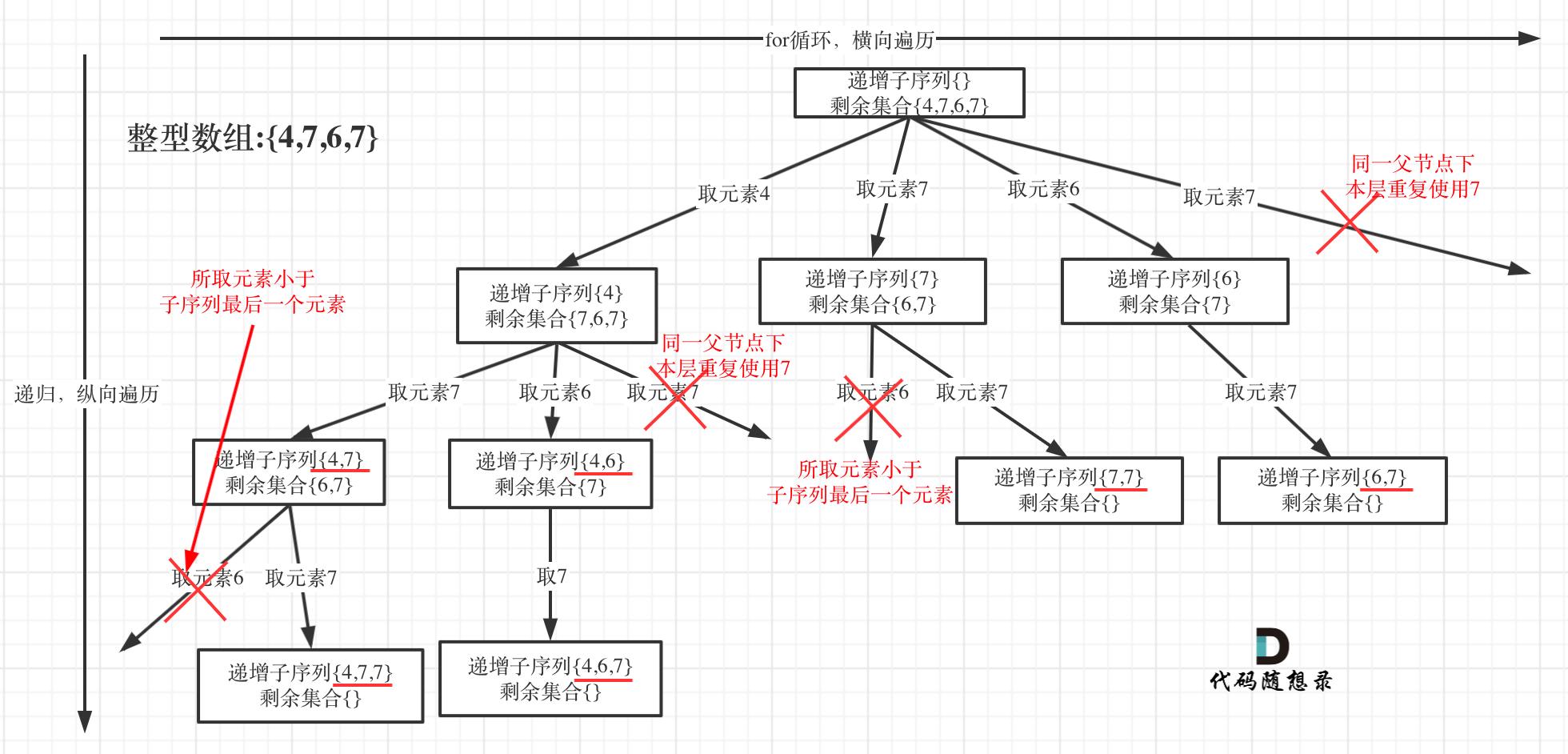
给定一个整型数组，任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。因此也就无法使用去重逻辑。

private List<Integer> path = new ArrayList<>();
private List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
    backTracking(nums,0);
    return result;
}

public void backTracking(int[] nums,int startIndex) {
    if(path.size() > 1) {
        result.add(new ArrayList<>(path));
        //注意此处不能加return，因为之后可能还有结果需加入结果集
    }

    int[] used = new int[201];  //这里使用数组来进行去重操作，题目说明数值范围在【-100,100】
    for(int i = startIndex; i < nums.length; i++) {
        if(!path.isEmpty() && path.get(path.size() - 1) > nums[i] || used[nums[i] + 100] == 1) {
            continue;
        }

        used[nums[i] + 100] = 1;    //记录这个元素在本层用过了，本层后面不能再用了。此处不用进行回溯是因为每一层都会有新的used来记录本层的重复元素
        path.add(nums[i]);
        backTracking(nums,i + 1); 
        path.remove(path.size() - 1);
    }
}

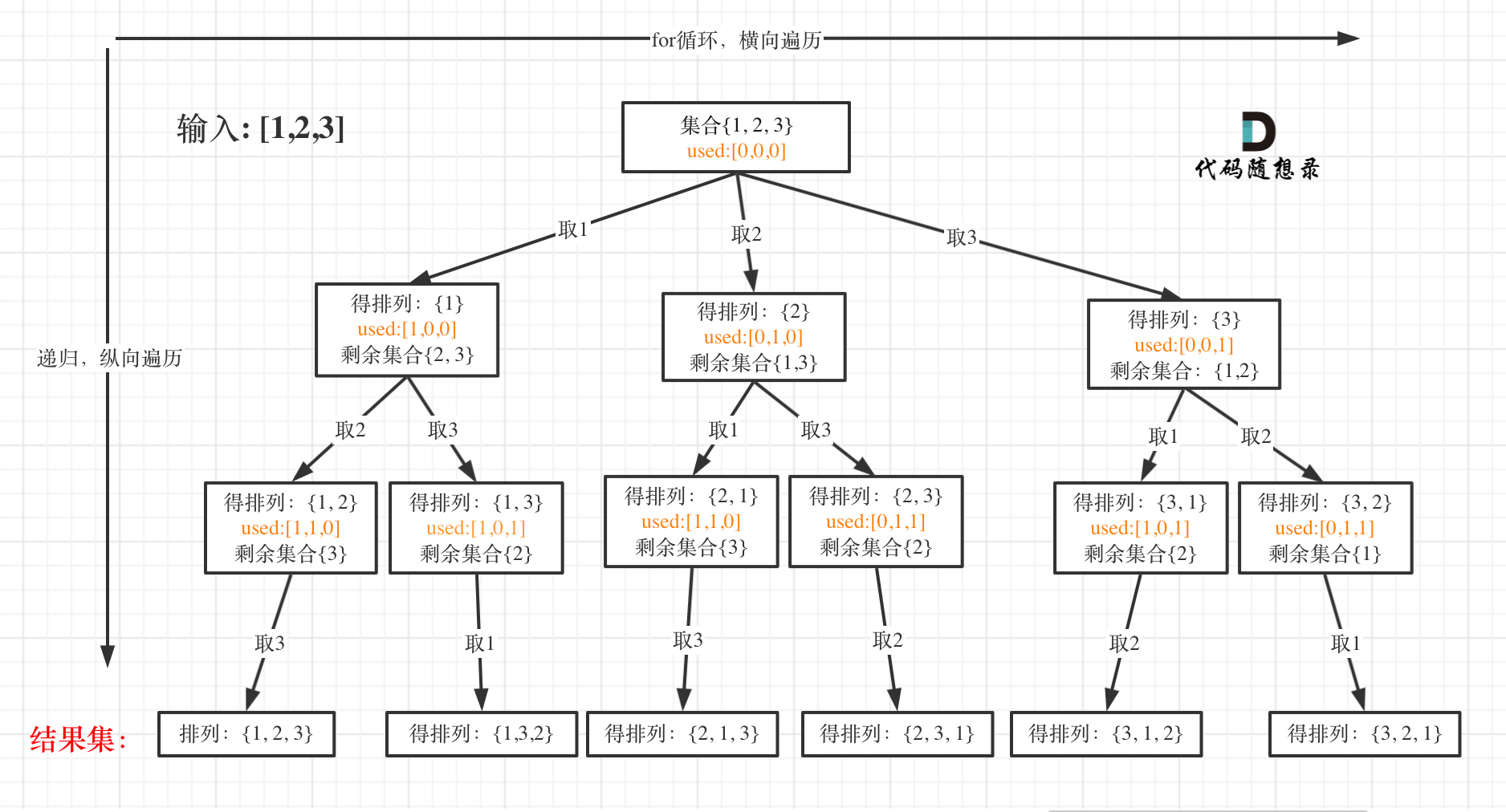
全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
    boolean[] used = new boolean[nums.length];
    backTraking(nums,used);
    return result; 
}

public void backTraking(int[] nums,boolean[] used) {
    //此时说明找到了一组
    if(path.size() == nums.length) {
        result.add(new ArrayList<>(path));
    }

    for(int i = 0; i < nums.length; i++) {
        if(used[i] == true) continue;   //path里已经收录的元素，直接跳过

        // 如果path中已有，则跳过
        /*if (path.contains(nums[i])) {
                continue;
            }*/ //解法二：通过判断path中是否存在数字，排除已经选择的数字，这样就可以省去used数组

        used[i] = true;
        path.add(nums[i]);
        backTraking(nums,used);
        path.remove(path.size() - 1);
        used[i] = false;
    }
}

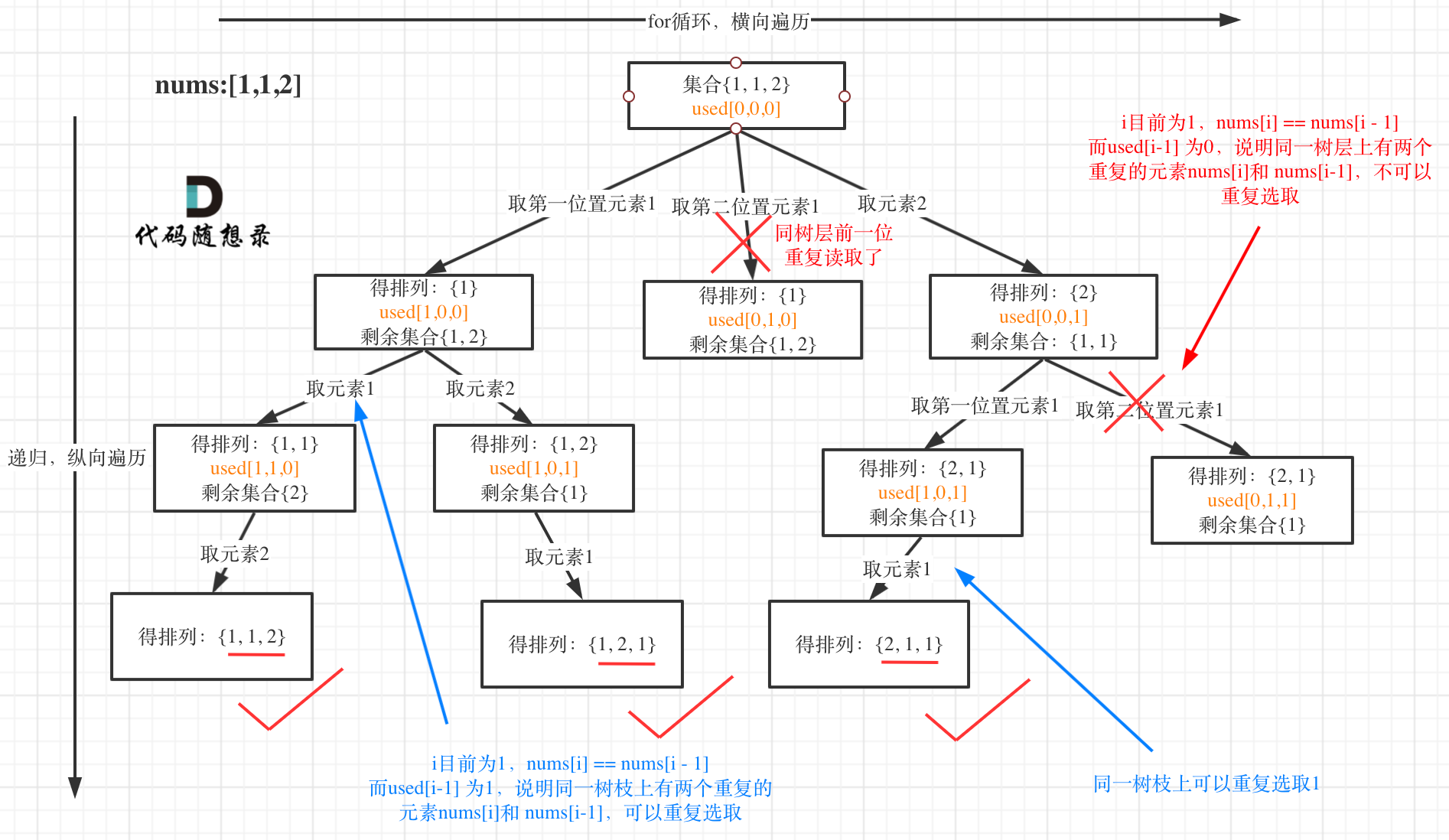
全排序II

给定一个可包含重复数字的序列nums，按任意顺序返回所有不重复的全排列。去重的套路都是一样的，要强调的是去重一定要对元素进行排序。

List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
    boolean[] used = new boolean[nums.length];
    Arrays.sort(nums);
    backTraking(nums,used);
    return result; 
}

public void backTraking(int[] nums,boolean[] used) {
    if(path.size() == nums.length) {
        result.add(new ArrayList<>(path));
    }

    for(int i = 0; i < nums.length; i++) {
        if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
            continue;
        }
        if(used[i] == false) {
            path.add(nums[i]);
            used[i] = true;
            backTraking(nums,used);
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }
}

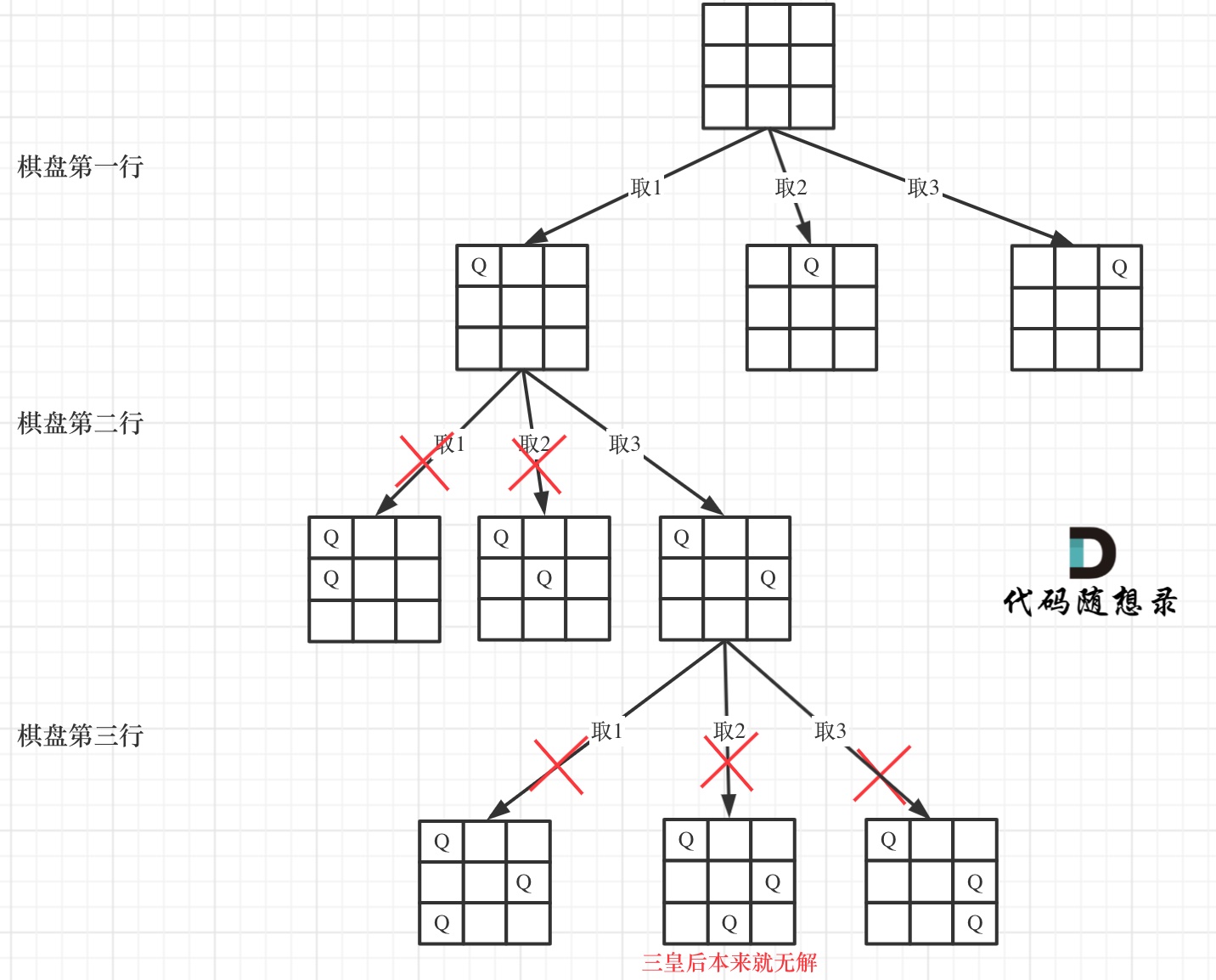
N皇后

给你一个整数n，返回所有不同的n皇后问题的解决方案。n皇后的约束条件：不能同行、不能同列、不能斜线。

List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
    char[][] chessboard = new char[n][n];
    for(char[] c : chessboard) {
        Arrays.fill(c,'.');
    }
    backTracking(n,0,chessboard);
    return res;
}
//n为输入的棋盘大小     row是当前递归到棋盘的第几行了
public void backTracking(int n,int row,char[][] chessboard) {
    if(row == n) {
        res.add(Array2List(chessboard));
        return;
    }

    for(int col = 0; col < n; ++col) {
        if(isValid(row,col,n,chessboard)) {     //验证放在此位置是否合法
            chessboard[row][col] = 'Q';         //放置皇后
            backTracking(n,row + 1,chessboard);
            chessboard[row][col] = '.';         //回溯，撤销皇后
        }
    }
}

public boolean isValid(int row,int col,int n,char[][] chessboard) {
    //检查列
    for(int i = 0; i < row; ++i) {
        if(chessboard[i][col] == 'Q') {     //相当于剪枝
            return false;
        }
    }

    //检查45度对角线
    for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
        if(chessboard[i][j] == 'Q') {
            return false;
        }
    }

    //检查135度对角线
    for(int i = row - 1,j = col + 1;i >= 0 && j <= n - 1;i--,j++) {
        if(chessboard[i][j] == 'Q') {
            return false;
        }
    }
    return true;
}

public List Array2List(char[][] chessboard) {
    List<String> list = new ArrayList<>();

    for(char[] c : chessboard) {
        list.add(String.copyValueOf(c));
    }
    return list;
}

括号生成

数字n代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

• 当前左右括号都有大于0个可以使用的时候，才产生分支；
• 产生分支的时候，只看当前是否还有左括号可以使用；
• 产生右分支的时候，还受到左分支的限制，右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候，才可以产生分支；
• 在左边和右边剩余的括号数都等于0的时候结算。

List<String> res = new ArrayList<>();
public List<String> generateParenthesis(int n) {
    if(n == 0) return res;
    StringBuilder path = new StringBuilder();
    dfs(path,n,n,res);
    return res;
}
public void dfs(StringBuilder path,int left,int right,List<String> res) {
    if(left == 0 && right == 0) {
        res.add(path.toString());
        return;
    }
    //剪枝
    if(left > right) {
        return;
    }
    if(left > 0) {
        path.append("(");
        dfs(path,left - 1,right,res);
        path.deleteCharAt(path.length() - 1);
    }
    if(right > 0) {
        path.append(")");
        dfs(path,left,right - 1,res);
        path.deleteCharAt(path.length() - 1);
    }
}

矩阵中的路径

给定一个m×n二维字符网格board和一个字符串单词word。如果word存在于网格中，返回true；否则，返回false。

• 递归参数：当前元素在矩阵board中的行列索引i和j，当前目标字符在word中的索引k。
• 终止条件：
  1. 返回false：行或列索引越界、当前矩阵元素与目标字符不同、当前矩阵元素已被访问过
  2. 返回true：当k=word.length() - 1，即字符串word已全部匹配完成。
• 递推工作：
  1. 标记当前矩阵元素：将board[i] [j]修改为空''，代表此元素已访问过，防止之后搜索时重复访问。
  2. 搜索下一单元格：超当前元素的上、下、左、右四个方向开启下层递归，使用或连接（代表只需找到一条可行路径就直接返回，不再做后序DFS），并记录结果至res
  3. 还原当前矩阵元素：将board[i] [j]元素还原至初始值，即word[k]
• 返回值：返回布尔变量res，代表是否搜索到目标字符串。

public boolean exist(char[][] board, String word) {
    char[] words = word.toCharArray();
    for(int i = 0; i < board.length; i++) {
        for(int j = 0; j < board[0].length; j++) {
            if(dfs(board,words,i,j,0)) return true;
        }
    }
    return false;
}
public boolean dfs(char[][] board,char[] word,int i, int j, int k) {
    if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
    if(k == word.length - 1) return true;
    board[i][j] = '\0';
    boolean res = dfs(board,word,i + 1,j,k + 1) || dfs(board,word,i - 1,j,k + 1) || dfs(board,word,i,j + 1,k + 1) || dfs(board,word,i,j - 1,k + 1);
    board[i][j] = word[k];
    return res;
}

所有可能的路径

给你一个有n个节点的有向无环图（DAG），请你找出所有从节点0到节点n-1的路径并输出。graph[i]是一个从节点i可以访问的所有节点的列表（即从节点i到节点graph[i] [j]存在一条有向边）。

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

深度优先搜索：

使用深度优先搜索的方式求出所有可能的路径。从0号点开始出发，使用栈记录路径上的点。每次遍历到点n-1，就将栈中记录的路径加入到答案中。特别地，因为本题中的图为有向无环图（DAG），搜索过程中不会反复遍历同一个点，因此无需判断当前点是否遍历过。

List<List<Integer>> result = new ArrayList<>();
Deque<Integer> stack = new ArrayDeque<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
    stack.offerLast(0);
    dfs(graph,0,graph.length - 1);
    return result;
}
public void dfs(int[][] graph,int index,int length) {
    if(index == length) {
        result.add(new ArrayList<>(stack));
        return;
    }
    for(int value : graph[index]) {
        stack.offerLast(value);
        dfs(graph,value,length);
        stack.pollLast();
    }
}